线面角与线线角20110721

A B

C H S M 线面角与线线角20110721

线面角：

直线和平面所成的角：（1）定义：（2）范围：[0,90] ；（3）求法；

1.如图, 四棱锥P-ABCD 的底面是AB=2, BC=2的矩形, 侧面PAB 是等边三角形, 且侧面

PAB ⊥底面ABCD.(Ⅰ)证明:BC ⊥侧面PAB;(Ⅱ)证明: 侧面PAD ⊥侧面PAB;(Ⅲ)求侧棱PC 与底面ABCD 所成角的大小;

练习：

1. 设△ABC 内接于⊙O ，其中AB 为⊙O 的直径，PA ⊥平面ABC 。

如图5cos ,:4:3,6

ABC PA AB ∠==求直线PB 和平面PAC 所成角的大小.

2．已知三棱锥P-ABC 的三条侧棱PA 、PB 、PC 两两垂直，D 是底面三角形内一点，且

∠DPA=450，∠DPB=600，则∠DPC=__________。

3．如图，四面体ABCS 中，SA ，SB ，SC 两两垂直，∠SBA=45°，∠SBC=60°，M 为AB 的中点，求：

（1）BC 与平面SAB 所成的角；（2）SC 与平面ABC 所成角的正弦值。只做第一小问，第二小问供有余力生做。

A B C D P

和m 异面线线角

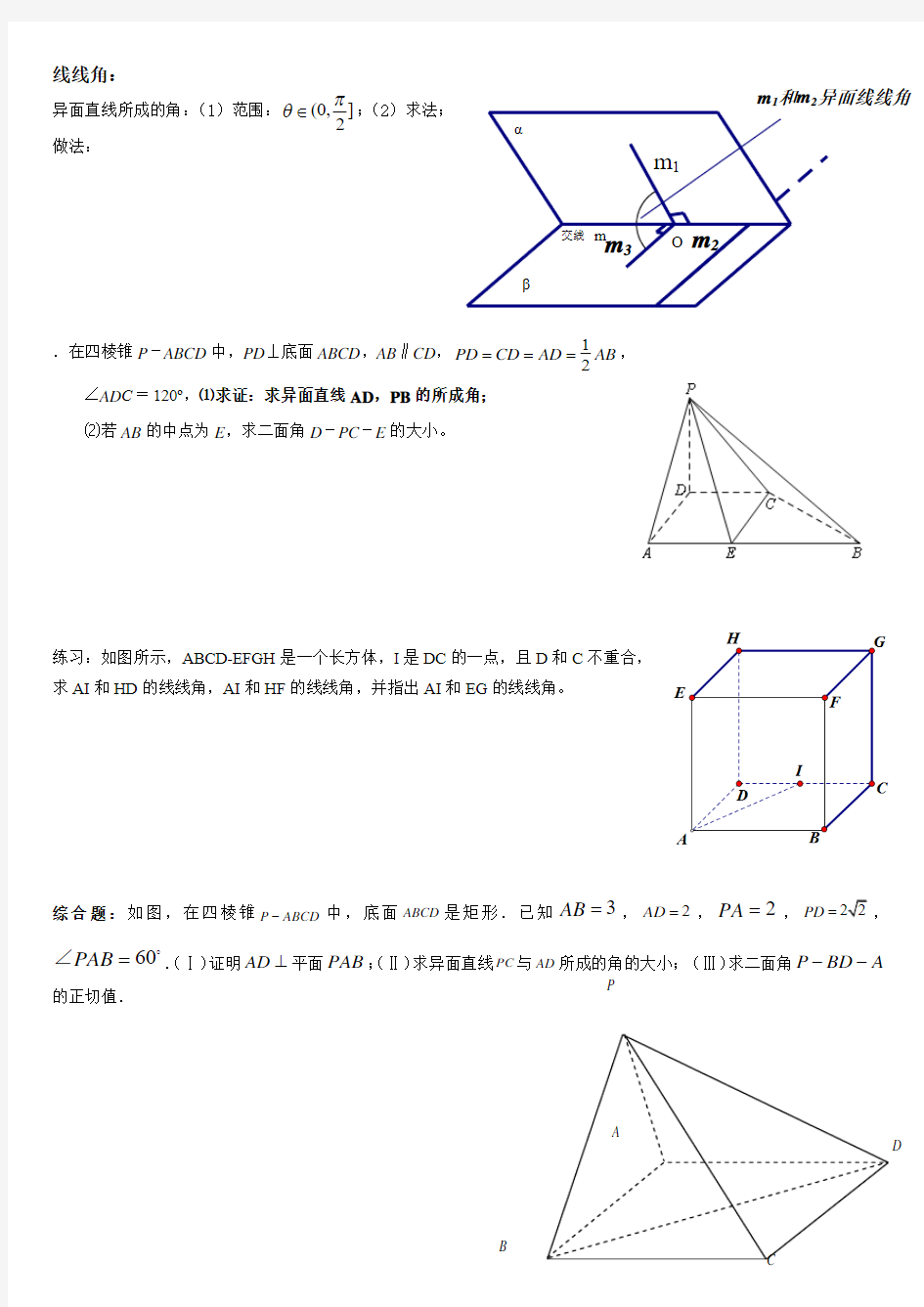
线线角：

异面直线所成的角：（1）范围：(0,

]2πθ∈；（2）求法； 做法：

．在四棱锥P －ABCD 中，PD ⊥底面ABCD ，AB ∥CD ，12

PD CD AD AB ===， ∠AD C ＝120o，⑴求证：求异面直线AD ，PB 的所成角；

⑵若AB 的中点为E ，求二面角D －PC －E 的大小。

练习：如图所示，ABCD-EFGH 是一个长方体，I 是DC 的一点，且D 和C 不重合， 求AI 和HD 的线线角，AI 和HF 的线线角，并指出AI 和EG 的线线角。

综合题：如图，在四棱锥P ABCD -中，底面ABCD 是矩形．已知3AB =，2AD =，2PA =

，PD =，60PAB = ∠．（Ⅰ）证明AD ⊥平面PAB ；（Ⅱ）求异面直线PC 与AD 所成的角的大小； （Ⅲ）求二面角P BD A --的正切值．

A B C D

P

高中数学线面角与线线角例题、习题-学生

线面角与线线角专练（小练习一）【知识网络】 1、异面直线所成的角：（1）范围：(0,]2π θ∈； （2）求法； 2、直线和平面所成的角：（1）定义：（2）范围：[0,90]o o ；（3）求法； 【典型例题】 例1：（1）在正方体1111ABCD A B C D -中，下列几种说法正确的是 （ ） A 、11AC AD ⊥ B 、11D C AB ⊥ C 、1AC 与DC 成45o 角 D 、11AC 与1B C 成60o 角 （2）在正方体AC 1中，过它的任意两条棱作平面，则能作得与A 1B 成300角的平面的个数为 （ ） A 、2个 B 、4个 C 、6个 D 、8个 （3）正六棱柱ABCDEF －A 1B 1C 1D 1E 1F 1底面边长是1，2则这个棱柱的侧 面对角线E 1D 与BC 1所成的角是 （ ） A ．90o B ．60o C ．45o D ．30o （4）在空间四边形ABCD 中，AB ⊥CD ，BC ⊥DA ，那么对角线AC 与BD 的位置关系是 。 （5）点AB 到平面α距离距离分别为12，20，若斜线AB 与α成030的角，则AB 的长等于__ ___. 例2：．如图：已知直三棱柱ABC —A 1B 1C 1，AB ＝AC ，F 为棱BB 1上一点，BF ∶FB 1＝2∶1，BF ＝BC ＝2a 。 （I ）若D 为BC 的中点，E 为AD 上不同于 A 、D 的任意一点，证明EF ⊥FC 1； （II ）试问：若AB ＝2a ，在线段AD 上的E 点能否使EF 与平面BB 1C 1C 成60°角，为什么？证明你的结论。 例3： 如图, 四棱锥P-ABCD 的底面是AB=2, BC =2的矩形, 侧面PAB 是等边三角形, 且侧面 PAB ⊥底面ABCD. (Ⅰ)证明:BC ⊥侧面PAB; (Ⅱ)证明: 侧面PAD ⊥侧面PAB; (Ⅲ)求侧棱PC 与底面ABCD 所成角的大小; A B C D P

线线角、线面角、二面角知识点及练习

线线角、线面角、面面角专题 一、异面直线所成的角 1.已知两条异面直线,a b ，经过空间任意一点O 作直线//,//a a b b ''，我们把a '与b '所成的锐角（或直角）叫异面直线,a b 所成的角。 2.角的取值范围：090θ<≤?； 垂直时，异面直线当b a ,900=θ。 例1.如图, 在直三棱柱111ABC A B C -中，13,4,5,4AC BC AB AA ==== ，点D 为AB 的中点异面直线1AC 与1B C 所成角的余弦值 二、直线与平面所成的角 1. 定义：平面的一条斜线和它在平面上的射影所成的锐角， 叫这条斜线和这个平面所成的角 2.角的取值范围：? ? ≤≤900θ。 _1 _A

例2. 如图、四面体ABCS 中，SA,SB,SC 两两垂直，∠SBA=45°, ∠SBC=60°, M 为 AB 的中 点，求（1）BC 与平面SAB 所成的角。 （2）SC 与平面ABC 所成的角的正切值。 一、 二面角： 1. 从一条直线出发的两个半平面所组成的图形叫做二 面角。这条直线叫做二面角的棱，这两个半平面叫做二面角的面。 2. 二面角的取值范围：? ? ≤≤1800θ 两个平面垂直：直二面角。 B M H S C A

3.作二面角的平面角的常用方法有六种： 1.定义法 ：在棱上取一点O ，然后在两个平面内分别作过棱上O 点的垂线。 2.三垂线定理法：先找到一个平面的垂线，再过垂足作棱的垂线，连结两个垂足即得二面角的平面角。 3.向量法：分别作出两个半平面的法向量，由向量夹角公式求得。二面角就是该夹角或其补角。 二面角一般都是在两个平面的相交线上，取恰当的点，经常是端点和中点。 例3.如图，E 为正方体ABCD －A 1B 1C 1D 1的棱CC 1的中点，求 (1)二面角111D C A D --所成的角的余弦值 (2)平面AB 1E 和底面C C BB 11所成锐角的正切值. A 1 D 1 B 1 C 1 E D B C A

空间中线线角,线面角,面面角成法原理和求法思路

D B A C α 空间中的夹角 福建屏南一中 李家有 QQ52331550 空间中各种角包括：异面直线所成的角、直线与平面所成的角以及二面角。 1、异面直线所成的角 （1）异面直线所成的角的范围是2 , 0(π 。求两条异面直线所成的角的大小一般方法是通过平行移动 直线，把异面问题转化为共面问题来解决。 具体步骤如下： ①利用定义构造角，可固定一条，平移另一条，或两条同时平移到某个特殊的位置，顶点选择在特殊的位置上； ②证明作出的角即为所求的角； ③利用解三角形来求角。简称为“作，证，求” 2、线面夹角 直线与平面所成的角的范围是]2 , 0[π 。求直线和平面所成的角用的是射影转化法。 具体步骤如下：（若线面平行，线在面内，线面垂直，则不用此法，因为角度不用问你也知道） ①找过斜线上一点与平面垂直的直线； ②连结垂足和斜足，得出斜线在平面的射影，确定出所求的角； ③把该角置于三角形中计算。 也是简称为“作，证，求” 注：斜线和平面所成的角，是它和平面内任何一条直线所成的一切角中的最小角，即若θ为线面角，β为斜线与平面内任何一条直线所成的角， 则有θβ≤；（这个证明，需要用到正弦函数的单调性，请跳过。在右图的解释为 BAD CAD ∠>∠） ） 2.1确定点的射影位置有以下几种方法： ①斜线上任意一点在平面上的射影必在斜线在平面的射影上； ②如果一个角所在的平面外一点到角的两边距离相等，那么这一点在平面上的射影在这个角的平分线上； 已知：如图，BAC ∠在一个平面α内， ,,PN AC PM AB PN PM ⊥⊥且＝（就是点P 到角 两边的距离相等）过P 作PO α⊥（说明点O 为P 点在面α内的射影） 求证：OAN OAM ∠∠＝ （OAN OAM ∠∠＝，所以AO 为BAC ∠的角平分线，所以点O 会在BAC ∠的角平分线上） 证明：PA ＝PA ，PN ＝PM ， 90PNA PMA ∠∠?＝＝ PNA PMA ∴???（斜边直角边定理） AN AM ∴＝ ① (PO NO MO PN PM α⊥? ?=?? 斜线长相等推射影长相等） ＝

线面角的计算方法

教师姓名 余永奇 学生姓名 洪 懿 上课时间 2014.11.15 辅导学科 数学 学生年级 高二 教材版本 人教版 课题名称 线面角，二面角的计算方法（文科） 本次学生 课时计划 第（10）课时 共（60）课时 教学目标 线面角的计算方法 教学重点 线面角的计算方法 教学难点 线面角的计算方法 教师活动 学生活动 上次作业完成情况(%) 一．检查作业完成情况，并讲解作业中存在的问题 二．回顾上次课辅导内容 三．知识回顾，整体认识 1、本章知识回顾 （1）空间点、线、面间的位置关系； （2）直线、平面平行的判定及性质； （3）直线、平面垂直的判定及性质。 2、本章知识结构框图 （二）整合知识，发展思维 1、刻画平面的三个公理是立体几何公理体系的基石，是研究空间图形问题，进行逻辑推理的基础。 公理1——判定直线是否在平面内的依据； 公理2——提供确定平面最基本的依据； 公理3——判定两个平面交线位置的依据； 公理4——判定空间直线之间平行的依据。 2、空间问题解决的重要思想方法：化空间问题为平面问题； 3、空间平行、垂直之间的转化与联系： 平面（公理1、公理2、公理3、公理4） 空间直线、平面的位置关系 直线与直线的位置关系 直线与平面的位置关系 平面与平面的位置关系 直线与直线平行 直线与平面平行 平面与平面平行

4、观察和推理是认识世界的两种重要手段，两者相辅相成，缺一不可。 典型例题： 线面夹角的计算 例1（2014浙江高考文科20题）如图，在四棱锥A-BCDE中，平面ABC⊥平面BCDE，∠CDE=∠BED =90°，AB=CD=2, DE=BE=1，AC=2. （Ⅰ）证明：AC⊥平面BCDE； （Ⅱ）求直线AE与平面ABC所成的角的正切值. 例2(2013浙江，文20)如图，在四棱锥P－ABCD中，PA⊥平面ABCD，AB＝BC＝2，AD＝CD＝7，PA ＝3，∠ABC＝120°，G为线段PC上的点． (1)证明：BD⊥平面APC； (43 3 ) (2)若G为PC的中点，求DG与平面APC所成的角的正切值； (3)若G满足PC⊥平面BGD，求PG GC 的值．(3/2) 直线与直线垂直直线与平面垂直平面与平面垂直

线线角和线面角

线线角和线面角 [重点]：确定点、斜线在平面内的射影。 [知识要点]： 一、线线角 1、定义：设a、b是异面直线，过空间一点O引a′//a,b′//b,则a′、b′所成的锐角(或直角),叫做异面直线a、b所成的角. 2、范围:(0,] 3. 向量知识： 对异面直线AB和CD (1)； (2) 向量和的夹角<,>(或者说其补角)等于异面直线AB 和CD的夹角； (3) 二、线面角 1、定义：平面的一条斜线和它在这个平面内的射影所成的锐角，斜线和平面所成角的范围是(0,). 2、直线在平面内或直线与平面平行，它们所成角是零角； 直线垂直平面它们所成角为， 3、范围: [0,]。 4、射影定理：斜线长定理：从平面外一点向这个平面所引的垂线段和斜线段中： （1）射影相等的两条斜线段相等，射影较长的斜线段也较长； （2）相等的斜线段的射影相等，较长的斜线段的射影也较长； （3）垂线段比任何一条斜线段都短。

5、最小角定理：平面的一条斜线与平面所成的角，是这条直线和平面内过斜足的直线所成的一切角中最小的角。 6、向量知识 （法向量法）与平面的斜线共线的向量和这个平面的一个法向量的夹角<,>(或者说其补角)是这条斜线与该平面夹角的余角. [例题分析与解答] 例1．如图所示，在棱长为a的正方体ABCD-A1B1C1D1中，求：异面直线BA1与AC所成的角. 分析：利用，求出向量的夹角,再根据异面直线BA1，AC所成角的范围确定异面直线所成角. 解：∵，， ∴ ∵AB⊥BC，BB1⊥AB，BB1⊥BC， ∴ ∴ 又 ∴ ∴ 所以异面直线BA1与AC所成的角为60°. 点评：求异面直线所成角的关键是求异面直线上两向量的数量积，而要求两向量的数量积，必须会把所求向量用空间的一组基向量来表示. 例2．如图(1)，ABCD是一直角梯形，AD⊥AB，AD//BC，AB=BC=a, AD=2a,且PA⊥平面ABCD，PD与平面ABCD成30°角.

高中数学线面角与线线角例题习题

线面角与线线角 【知识网络】 1、异面直线所成的角：（1）范围：(0, ]2 π θ∈； （2）求法； 2、直线和平面所成的角：（1）定义：（2）范围：[0,90]o o ；（3）求法； 3、一些常见模型中的角之间的关系。 【典型例题】 例1：（1）在正方体1111ABCD A B C D -中，下列几种说法正确的是 （ ） A 、11AC AD ⊥ B 、11D C AB ⊥ C 、1AC 与DC 成45o 角 D 、11AC 与1B C 成60o 角 答案：D 。解析：A 1C 1与AD 成45°，D 1C 1与AB 平行，AC 1与DC 所成角的正切为 2 2 。 （2）在正方体AC 1中，过它的任意两条棱作平面，则能作得与A 1B 成300角的平面的个数为 （ ） A 、2个 B 、4个 C 、6个 D 、8个 答案：B 。解析：平面A 1ACC 1，平面BB 1D 1D ，平面ABC 1D 1，平面A 1D 1CC 1。 （3）正六棱柱ABCDEF －A 1B 1C 1D 1E 1F 1底面边长是1，2则这个棱柱的侧 面对角线E 1D 与BC 1所成的角是 （ ） A ．90o B ．60o C ．45o D ．30o 答案：B 。解析将BC 1平移到E 1F 即可。 （4）在空间四边形ABCD 中，AB ⊥CD ，BC ⊥DA ，那么对角线AC 与BD 的位置关系是 。 答案：AC ⊥BD 。解析：过A 作AH ⊥平面BCD ，垂足为H ，因为CD ⊥AB ，BC ⊥AD ，所以CD ⊥BH ，BC ⊥DH ，故H 为△BCD 的垂心，从而BD ⊥CH ，可得BD ⊥AC 。 （5）点AB 到平面α距离距离分别为12，20，若斜线AB 与α成030的角，则AB 的长等于__ ___. 答案：16或64。解析：分A 、B 在平面α的同侧和异侧进行讨论。 例2：．如图：已知直三棱柱ABC —A 1B 1C 1，AB ＝AC ，F 为棱BB 1上一点，BF ∶FB 1 ＝2∶1，BF ＝BC ＝2a 。 （I ）若D 为BC 的中点，E 为AD 上不同于 A 、D 的任意一点，证明EF ⊥FC 1； （II ）试问：若AB ＝2a ，在线段AD 上的E 点能否使EF 与平面BB 1C 1C 成60°角，为什么？证明你的结论。

§52 线线角与线面角(教案)

B 1 D 1 A D C 1 B C A 1 §线线角与线面角(教案) 一、复习目标 1.理解异面直线所成角的概念,并掌握求异面直线所成角的常用方法． 2.理解直线与平面所成角的概念，并掌握求线面角常用方法． 3.掌握求角的计算题步骤是“一作、二证、三计算”,思想方法是将空间图形转化为平面图形即“降维” 的思想方法. 二、课前预习 1.在空间四边形ABCD中，AD=BC=2, E、F分别为AB、CD的中点且EF=3，AD、BC所成的角 为. 2.如图,在长方体ABCD-A1B1C1D1中，B1C和C1D与底面所成的角分别为60ο和45ο，则异面直线B1C 和C1D所成角的余弦值为( ) (A). 4 6 (B). 3 6 (C). 6 2 (D). 6 3 3.平面α与直线a所成的角为 3 π ,则直线a与平面α内所有直线所成的角的取值范围是． 4.如图,ABCD是正方形,PD⊥平面ABCD,PD=AD,则PA与BD所成的角的度数为 ( ) (A).30ο(B).45ο(C).60ο(D).90ο 5.有一个三角尺ABC,∠A=30ο, ∠C=90ο,BC是贴于桌面上, 当三角尺与桌面成45ο角时,AB边与桌面所成角的正弦值 是． 三、典型例题 例1.(96·全国) 如图,正方形ABCD所在平面与正方形ABEF所在平面成60ο角,求异面直线AD与BF 所成角的余弦值. 备课说明:1.求异面直线所成的角常作出所成角的平面图形.作法有: ①平移法:在异面直线的一条上选择“特殊点”,作另一条直线平行线 或利用中位线.②补形法:把空间图形补成熟悉的几何体,其目的在于容 易发现两条异面直线的关系. 2.解立几计算题要先作出所求的角,并要有严格的推理论证过 程,还要有合理的步骤. A C B D B P C D A C B F E

线线角_线面角_二面角的讲义

B 1 D 1 A D C 1 B C A 1线线角与线面角 一、课前预习 1.在空间四边形ABCD 中，AD=BC=2, E 、F 分别为AB 、CD 的中点且EF=3，AD 、BC 所成的角为 . 2.如图,在长方体ABCD-A1B1C1D1中 ，B1C 和C1D 与底面所成的 角分别为60ο和45ο，则异面直线B1C 和C1D 所成角的余弦值为 ( ) (A). 46 (B).36 (C).62 (D).63 3.平面α与直线a 所成的角为3π ,则直线a 与平面α内所有直 线所成的角的取值范围是 ． 4.如图,ABCD 是正方形,PD ⊥平面ABCD,PD=AD,则PA 与BD 所成的角的度数为 (A).30ο (B).45ο (C).60ο (D).90ο 5.有一个三角尺ABC,∠A=30ο, ∠C=90ο,BC 是贴于桌面上, 当三角尺与桌面成45ο角时,AB 边与桌面所成角的正弦值 是 ． 二、典型例题 例1.(96·全国) 如图,正方形ABCD 所在平面与正方形 ABEF 所在平面成60ο角,求异面直线AD 与BF 所成角的余弦值. 【备课说明:1.求异面直线所成的角常作出所成角的平 A C B D B P C D A C B

面图形.作法有: ①平移法:在异面直线的一条上选择“特殊点”,作另一条直线平行线或利用中位线.②补形法:把空间图形补成熟悉的几何体,其目的在于容易发现两条异面直线的关系.2.解立几计算题要先作出所求的角,并要有严格的推理论证过程,还要有合理的步骤.】 例2.如图在正方体AC1中, (1) 求BC1与平面ACC1A1所成的角; (2) 求A1B1与平面A1C1B 所成的角. 备课说明:求直线与平面所成角的关键是找直线在此平面上的射影,为此必须在这条直线上找一点作平面的垂线. 作垂线的方法常采用:①利用平面垂直 的性质找平面的垂线.②点的射影在面内的特殊位置. 例3. 已知直三棱住ABC-A1B1C1,AB=AC, F 为棱BB1上一点,BF ∶FB1=2∶1, BF=BC=a 2. (1)若D 为BC 的中点,E 为线段AD 上不同于A 、D 的任意一点,证明：EF ⊥FC1; (2)试问:若AB=a 2,在线段AD 上的E 点能否使EF 与平面BB1C1C 成60ο角,为什么?证明你的结论. 备课说明:这是一道探索性命题,也是近年高考热点问题,解 决这类问题,常假设命题成立,再研究是否与已知条件矛盾, 从而判断命题是否成立. 一、知识与方法要点： 1．斜线与平面所成的角就是斜线与它在平面内的射影的夹角。求斜线与平面所成的角关键是找到斜线在平面内的射影，即确定过斜 A D C 1 D 1 A 1 B 1 C B A 1C B A B 1 D C 1 E F

线线角与线面角

线线角与线面角 线线,线面,面面的平行与垂直,异面直线所成角,直线与平面所成角 异面直线所成角,直线与平面所成角 知识整合: 1.转化思想:将异面直线所成的角,直线与平面所成的角转化为平面角,然后解三角形;??⊥?⊥?⊥线线平行线面平行面面平行,线线线面面面 2.求角的三个步骤:一猜,二证,三算.猜是关键,在作线面角时,利用空间图形的平行,垂直,对称关系,猜斜线上一点或斜线本身的射影一定落在平面的某个地方,然后再证 热点题型1 例1、如图, 在直三棱柱111ABC A B C -中， 13,4,5,4AC BC AB AA ==== ，点D 为AB 的 中点 (Ⅰ)求证1AC BC ⊥; (Ⅱ) 求证11AC CDB 平面; (Ⅲ)求异面直线1AC 与1B C 所成角的余弦值 解析;异面直线所成角的平面角顶点O 的选取一般 选在两异面直线的端点处,初学者或观察能力有限者可采用穷举法,实行逐个端点考察,也有取在某线段的中点处. 解：（I ）直三棱柱ABC －A 1B 1C 1，底面三边长AC=3，BC=4AB=5， ∴ AC ⊥BC ，且BC 1在平面ABC 内的射影为BC ，∴ AC ⊥BC 1； （II ）设CB 1与C 1B 的交点为E ，连结DE ，∵ D 是AB 的中点，E 是BC 1的中点，∴ DE//AC 1， ∵ DE ?平面CDB 1，AC 1?平面CDB 1，∴ AC 1//平面CDB 1； （III ）∵ DE//AC 1，∴ ∠CED 为AC 1与B 1C 所成的角， 在△CED 中，ED=21AC 1=25，CD=21 AB=2 5， CE=2 1 CB 1=22， ∴ 8cos 5 5 22 CED ∠= = ?， 1 A 1 A

高考数学线线角与线面角复习

第5课时线线角与线面角 ?要点·疑点·考点 ?课前热身 ?能力·思维·方法 ?延伸·拓展 ?误解分析

要点·疑点·考点 1.线线角 (2)范围：?? ? ??20π，(1)定义：设a 、b 是异面直线，过空间任一点O 引，则所成的锐角(或直角)，叫做异面直线a 、b 所成的角. b a ''，a 'b b a ////'，

2.线面角 (3)范围：?? ????20π，(1)定义：平面的一条斜线和它在平面上的射影所成的锐角，叫这条斜线和这个平面所成的角 (2)若直线l ⊥平面α，则l 与α所成角为直角 若直线l ∥平面α，或直线l 平面α，则l 与α所成角为0° ?

(4)射影定理：从平面α外一点向这个平面所引的 垂线段和斜线段中： ①射影相等的两条斜线段相等，射影较长的斜线 段也较长； ②相等的斜线段的射影相等，较长的斜线段的射 影也较长； ③垂线段比任何一条斜线段都短 (5)最小角定理：斜线和平面所成的角，是这条斜 线和平面内过斜足的直线所成的一切角中的最小 的角. 返回

2. 相交成90°的两条直线与一个平面所成的角分别是30°与45°，则这两条直线在该平面内的射影所成角的正弦值为( )(A) (B) (C) (D) 332336261. 平面α的斜线与α所成的角为30°，则此斜线和α内所有不过斜足的直线中所成的角的最大值是( )(A)30°(B)60°(C)90°(D)150° 课前热身 C C

3.如图，正方形ABCD所在平面与正方形ABEF所 在的平面成60°的二面角，则异面直线 AD与BF所 成角的余弦值是___________. 4 2

线线角、线面角,二面角(高考立体几何法宝)

1 A 1 B 1 C 1 D A B C D E F G 线线角、线面角、二面角的求法 1.空间向量的直角坐标运算律： ⑴两个非零向量与垂直的充要条件是 1122330a b a b a b a b ⊥?++= ⑵两个非零向量a 与b 平行的充要条件是 a ·b =±|a ||b | 2.向量的数量积公式 若a 与b 的夹角为θ(0≤θ≤π),且123(,,)a a a a =，123(,,)b b b b =,则 （1）点乘公式： ·=|||| cos θ （2）模长公式：则2 12||a a a a a =?=++2 ||b b b b =?=+ （3）夹角公式：2 cos ||||a b a b a b a ??==?+ （4）两点间的距离公式：若111(,,)A x y z ，222(,,)B x y z ，则 2 ||(AB AB ==,A B d = ①两条异面直线a 、b 间夹角0,2πα?? ∈ ??? 在直线a 上取两点A 、B ，在直线b 上取两点C 、D ，若直线a 与b 的夹角为θ，则cos |cos ,|AB CD θ=<>= 例1 (福建卷)如图，长方体ABCD —A 1B 1C 1D 1中，AA 1=AB =2，AD =1，点E 、F 、G 分别是DD 1、 AB 、CC 1的中点，则异面直线A 1E 与GF 所成的角是（ ） A ．5 15arccos B ． 4 π C ．510 arccos D ．2 π （向量法，传统法）

P B C A 例 2 (2005年全国高考天津卷)如图，PA ⊥平面ABC ，90ACB ∠=?且 PA AC BC a ===，则异面直线PB 与AC 所成角的正切值等于_____． 解：（1）向量法 （2）割补法：将此多面体补成正方体'''DBCA D B C P -，PB 与AC 所成的角的大小即此正方体主对角线PB 与棱BD 所成角的大小，在Rt △PDB 中 ，即 tan PD DBA DB ∠= =． 点评：本题是将三棱柱补成正方体'''DBCA D B C P - ②直线a 与平面α所成的角0,2πθ?? ∈ ??? (重点讲述平行与垂直的证明) 可转化成用向量→ a 与平面α的法向量→ n 的夹角ω表示，由向量平移得：若 ππ（图）；若ππ 平面α的法向量→ n 是向量的一个重要内容，是求直线与平面所成角、求点到平面距离的必备工具.求平面法向量的一般步骤： (1)找出(求出)平面内的两个不共线的向量的坐标111222(,,),(,,)a a b c b a b c == (2)设出平面的一个法向量为(,,)n x y z = (3)根据法向量的定义建立关于x,y,z 的方程组(0a < (4)解方程组，取其中的一组解，即得法向量。 图1－ 图1－ 图1－ 1 D 1 B 1 C P D B C A

线线角_线面角_二面角的讲义

B 1D 1A D C 1 B C A 1 线线角与线面角 一、课前预习 1.在空间四边形ABCD 中，AD=BC=2, E 、F 分别为AB 、CD 的中点且EF=3，AD 、BC 所成的角为 . 2.如图,在长方体ABCD-A1B1C1D1中 ，B1C 和C1D 与底面所成的角分别为60ο和45ο，则异面直线B1C 和C1D 所成角的余弦值为 ( ) (A). 46 (B).36 (C).62 (D).63 3.平面α与直线a 所成的角为3π ,则直线a 与平面α所有直线所成的角的取值围是 ． 4.如图,ABCD 是正方形,PD ⊥平面ABCD,PD=AD,则PA 与 BD 所成的角的度数为 (A).30ο (B).45ο (C).60ο (D).90ο 5.有一个三角尺ABC,∠A=30ο, ∠C=90ο,BC 是贴于桌面上, 当三角尺与桌面成45ο角时,AB 边与桌面所成角的正弦值 是 ． 二、典型例题 例1.(96·全国) 如图,正方形ABCD 所在平面与正方形 ABEF 所在平面成60ο角,求异面直线AD 与BF 所成角的余弦值. 【备课说明:1.求异面直线所成的角常作出所成角的平A C B D B P C D A C B

面图形.作法有: ①平移法:在异面直线的一条上选择“特殊点”,作另一条直线平行线或利用中位线.②补形法:把空间图形补成熟悉的几何体,其目的在于容易发现两条异面直线的关系.2.解立几计算题要先作出所求的角,并要有严格的推理论证过程,还要有合理的步骤.】 例2.如图在正方体AC1中, (1) 求BC1与平面ACC1A1所成的角; (2) 求A1B1与平面A1C1B 所成的角. 备课说明:求直线与平面所成角的关键是找直线在 此平面上的射影,为此必须在这条直线上找一点作 平面的垂线. 作垂线的方法常采用:①利用平面垂直 的性质找平面的垂线.②点的射影在面的特殊位置. 例 3. 已知直三棱住ABC-A1B1C1,AB=AC, F 为棱BB1上一点,BF ∶FB1=2∶1, BF=BC=a 2. (1)若D 为BC 的中 点,E 为线段AD 上不同于A 、D 的任意一点,证明：EF ⊥FC1; (2)试问:若AB=a 2,在线段AD 上的E 点能否 使EF 与平面BB1C1C 成60ο角,为什么?证明你的结论. 备课说明:这是一道探索性命题,也是近年高考热点问题,解 决这类问题,常假设命题成立,再研究是否与已知条件矛盾, 从而判断命题是否成立. 一、知识与方法要点： 1．斜线与平面所成的角就是斜线与它在平面的射影的夹角。求斜线与平面所成的角关键是找到斜线在平面的射影，即确定过斜线上A D C 1D 1A 1B 1C B A 1C B A B 1D C 1E F

线线角与线面角

线线角和线面角 ［重点］:确定点、斜线在平面内的射影。 ［知识要点］: 一、线线角 1、定义：设a 、b 是异面直线，过空间一点 O 引a ' 〃a,b '则/域；b 所成的锐角（或直角）， 叫 做异面直线a 、b 所成的角. 3. 向量知识： 对异面直线AB 和CD ⑵ 向量二_和匚匸 的夹角＜_」，「「「： ＞（或者说其补角）等于异面直线 AB 和CD 的夹角; （3）..”厂，二：二「二 ■-- 二、线面角 1、定义：平面的一条斜线和它在这个平面内的射影所成的锐角，斜线和平面所成角的范围 是(0, _ ). 2、直线在平面内或直线与平面平行，它们所成角是零角; 直线垂直平面它们所成角为 - 3、范围:［0,二］ 4、射影定理：斜线长定理：从平面外一点向这个平面所引的垂线段和斜线段中: （1） 射影相等的两条斜线段相等，射影较长的斜线段也较长； （2） 相等的斜线段的射影相等，较长的斜线段的射影也较长； 2、范围 7T 一

（3）垂线段比任何一条斜线段都短。

5、最小角定理：平面的一条斜线与平面所成的角，是这条直线和平面内过斜足的直线所成 的一切角中最小的角。 6、向量知识 （法向量法） ■* -f * 与平面的斜线共线的向量 显和这个平面的一个法向量 J 的夹角V 」，一1 >（或 者说其补角）是这条斜线与该平面夹角的余角 ［例题分析与解答］ 例1 ?如图所示，在棱长为 a 的正方体ABCD-A 1B 1C 1D 1中，求：异面直线 BA 1与AC 所成 的角. ■- - -11! ■',再根据异面直线 BA 1，AC 所成角的范围确定异面直线所成角 解：???】，—-匸二 ， -!<■'.：― 二.'：： =B T AB+BA BC+BB[ AB+BB[ BC ?/ AB 丄 BC ，BB 1 丄 AB ，BB 1± BC ， ...「 i,T-； I, BB] BSC BA AB = -a\ ...二小 cos < BApAC >= — ---------- =-— ...-_三〔13二- 所以异面直线 BA i 与AC 所成的角为60°. 点评：求异面直线所成角的关键是求异面直线上两向量的数量积，而要求两向量的数量积, 必须会把所求向量用空间的一组基向量来表示 例2.如图⑴，ABCD 是一直角梯形， AD 丄AB ，AD//BC ，AB=BC=a, AD=2a,且PA 丄平面 ABCD ，PD 与平面 ABCD 成30。角. 分析: 利用〔［厂「J _ \ J - 的夹角

空间中线线角,线面角,面面角成法原理与求法思路教学资料

空间中线线角,线面角,面面角成法原理与求 法思路

D B A C α 空间中的夹角 福建屏南一中 李家有 QQ52331550 空间中各种角包括：异面直线所成的角、直线与平面所成的角以及二面角。 1、异面直线所成的角 （1）异面直线所成的角的范围是2 ,0(π。求两条异面直线所成的角的大小一般方法是通过平行移动直线，把异面问题转化为共面问题来解决。 具体步骤如下： ①利用定义构造角，可固定一条，平移另一条，或两条同时平移到某个特殊的位置，顶点选择在特殊的位置上； ②证明作出的角即为所求的角； ③利用解三角形来求角。简称为“作，证，求” 2、线面夹角 直线与平面所成的角的范围是2 ,0[π。求直线和平面所成的角用的是射影转化法。 具体步骤如下：（若线面平行，线在面内，线面垂直，则不 用此法，因为角度不用问你也知道） ①找过斜线上一点与平面垂直的直线； ②连结垂足和斜足，得出斜线在平面的射影，确定出所求的 角； ③把该角置于三角形中计算。 也是简称为“作，证，求” 注：斜线和平面所成的角，是它和平面内任何一条直线所成的一切角中的最小角，即若θ为线面角，β为斜线与平面内任何一条直线所成的角，则有θβ≤；（这个证明，需要用到正弦函数的单调性，请跳过。在右图的解释为 BAD CAD ∠>∠）

） 2.1确定点的射影位置有以下几种方法： ①斜线上任意一点在平面上的射影必在斜线在平面的射影上； ②如果一个角所在的平面外一点到角的两 边距离相等，那么这一点在平面上的射影在这 个角的平分线上； 已知：如图，BAC ∠在一个平面α内， ,,PN AC PM AB PN PM ⊥⊥且＝（就是点P 到 角两边的距离相等）过P 作PO α⊥（说明点 O 为P 点在面α内的射影） 求证：OAN OAM ∠∠＝ （OAN OAM ∠∠＝，所以AO 为BAC ∠的角平分线，所以点O 会在BAC ∠的角平分线上） 证明：PA ＝PA ，PN ＝PM ，90PNA PMA ∠∠?＝＝ PNA PMA ∴???（斜边直角边定理） AN AM ∴＝ ① (PO NO MO PN PM α⊥??=?? 斜线长相等推射影长相等）＝ O AN AM AO AO AMO ANO NAO MAO OM N ???????∠∠??? ＝＝＝＝ 所以，点P 在面的射影为BAC ∠的角平分线上。 ③如果一条直线与一个角的两边的夹角相等，那么这一条直线在平面上的射影在这个角的平分线上；

《直线与平面所成角复习课——线面角的三种常见求法》教案

直线与平面所成角复习课（2） ——线面角的三种常见求法一、教学内容解析 新课标立体几何内容较大纲教材变化大，三垂线及其逆定理作为阅读教材，对于有关线、面的垂直的求解方式方法带来很大的改变，对求解二面角及线面角的方式方法也带来很大的改变。对我校大部分学生而言，二面角求解要求属于了解层次，斜线与平面角所成的角属于理解与掌握层次，“求解线面角”变成我校学生学习立体几何有关角的计算最难的一个问题。特别是教材中对线在平面上的射影这一概念比较弱化，点面距离的概念在教材中已经退化，我校学生学习线面角主要方法就是定义法。那如何化解难点，使学生能够有条不紊的找出线面角并求解，成为这堂课的重中之重。 二、教学目标设置 1、知识与技能：正确认识直线与平面所成角的概念，能够利用面面垂直的性质找出已知平面的垂线从而找出线面角，能够利用向量法和等体积法帮助求解线面角。 2、过程与方法： （1）空间想象能力：认识直线与平面的位置关系，遵循从实图和简单的几何体入手，逐步培养学生的几何直观和空间想象能力。 （2）转化的思想方法：在二维与三维空间的转化及线面角与线线角的转化过程中，体现出转化的思想方法。 （3）逻辑思维与运算能力：通过对线面角大小的求解，加强算中有证，以证助算，以培养学生的逻辑思维能力及运算能力。 3、情感、态度与价值观：体验概念的形成过程，培养创新意识和数学应用意识，提高学习数学的兴趣。 三、学生学情分析 我班学生“偏文”，尤其是女生的空间想象能力很弱，拿到立体几何题恨不得道道用向量法求解，因而忽视了定义法的重要性。学生在寻找线面角的过程中往往毫无头绪无从下手，缺少应有的逻辑推理能力和空间想象能力，不喜欢或不擅长添加复杂的辅助线帮助找角和证明。本节课旨在打开他们的解题思路，将求解过程规范化，有序化，从而能够进一步提高他们求解立体几何有关角的计算能力。 四、教学策略分析 由于这是一节复习课，所以我选择在前一节课留给他们一道简单而又经典的线面角问题，让他们自由发挥，各尽所能。然后，我挑选几位同学的做法，就他们的解题思路予以细节上的纠正和方法的总结。再之后，留给他们大段的思考整理时间，并给予一道类似但难度有所上升的题目交给他们再次求解，要求尽量用三种方法解答出来。整节课堂基本由学生们自己回忆，自己思考，自己讨论和总结。当然，线面角的方法复习并不是一蹴而就的，还需要不断地润色和努力。 五、教学过程 前情提要：

空间中线线角、线面角、面面角成法原理与求法思路

D B A C α 空间中的夹角 空间中各种角包括：异面直线所成的角、直线与平面所成的角以及二面角。 1、异面直线所成的角 （1）异面直线所成的角的范围是]2,0(π 。求两条异面直线所成的角的大小一般方法是通过平行移动 直线，把异面问题转化为共面问题来解决。 具体步骤如下： ①利用定义构造角，可固定一条，平移另一条，或两条同时平移到某个特殊的位置，顶点选择在特殊的位置上； ②证明作出的角即为所求的角； ③利用解三角形来求角。简称为“作，证，求” 2、线面夹角 直线与平面所成的角的范围是]2,0[π 。求直线和平面所成的角用的是射影转化法。 具体步骤如下：（若线面平行，线在面内，线面垂直，则不用此法，因 为角度不用问你也知道） ①找过斜线上一点与平面垂直的直线； ②连结垂足和斜足，得出斜线在平面的射影，确定出所求的角； ③把该角置于三角形中计算。 也是简称为“作，证，求” 注：斜线和平面所成的角，是它和平面内任何一条直线所成的一切角中的最小角，即若θ为线面角，β为斜线与平面内任何一条直线所成的角，则有θβ≤；（这个证明，需要用到正弦函数的单调性，请跳过。在右图的解释为 BAD CAD ∠>∠） ） 2.1确定点的射影位置有以下几种方法：

①斜线上任意一点在平面上的射影必在斜线在平面的射影上； ②如果一个角所在的平面外一点到角的两边距离 相等，那么这一点在平面上的射影在这个角的平分线 上； 已知：如图，BAC ∠在一个平面α内， ,,PN AC PM AB PN PM ⊥⊥且＝（就是点P 到角 两边的距离相等）过P 作PO α⊥（说明点O 为P 点在面α内的射影） 求证：OAN OAM ∠∠＝ （OAN OAM ∠∠＝，所以AO 为BAC ∠的角平分线，所以点O 会在BAC ∠的角平分线上） 证明：Q PA ＝PA ，PN ＝PM ，90PNA PMA ∠∠?＝＝ PNA PMA ∴???（斜边直角边定理） AN AM ∴＝ ① (PO NO MO PN PM α⊥??=?? 斜线长相等推射影长相等）＝ O AN AM AO AO AMO ANO NAO MAO OM N ???????∠∠??? ＝＝＝＝ 所以，点P 在面的射影为BAC ∠的角平 分线上。 ③如果一条直线与一个角的两边的夹角相等，那么这一条直线在平面上的射影在这个角的平分线 上； 已知：如图，BAC ∠在一个平面α内 PAN PAM ∠∠＝（斜线AP 与BAC ∠的两边 AB AC ，所成角相等）

线面角的几种求法

线面角的三种求法 河北 王学会 1．直接法 ：平面的斜线与斜线在平面内的射影所成的角即为直线与平面所成的角。通常是解由斜线段，垂线段，斜线在平面内的射影所组成的直角三角形，垂线段是其中最重要的元素，它可以起到联系各线段的作用。 例1 （ 如图1 ）四面体ABCS 中，SA,SB,SC 两两垂直，∠SBA=45°, ∠SBC=60°, M 为 AB 的中点，求（1）BC 与平面SAB 所成的角。 （2）SC 与平面ABC 所成的角。 解:（1） ∵SC ⊥SB,SC ⊥SA, B M H S C A 图1 ∴SC ⊥平面SAB 故 SB 是斜线BC 在平面SAB 上的射影， ∴∠SBC 是直线BC 与平面SAB 所成的角为60°。 （2） 连结SM,CM ，则SM ⊥AB, 又∵SC ⊥AB,∴AB ⊥平面SCM, ∴面ABC ⊥面SCM 过S 作SH ⊥CM 于H, 则SH ⊥平面ABC ∴CH 即为 SC 在面ABC 内的射影。 ∠SCH 为SC 与平面ABC 所成的角。 sin ∠SCH=SH ／SC ∴SC 与平面ABC 所成的角的正弦值为√7／7 （“垂线”是相对的，SC 是面 SAB 的垂线，又是面 ABC 的斜线. 作面的垂线常根据面面垂直的性质定理，其思路是：先找出与已知平面垂直的平面，然后一面内找出或作出交线的垂线，则得面的垂线。） 2. 利用公式sin θ=h ／ι 其中θ是斜线与平面所成的角， h 是 垂线段的长，ι是斜线段的长，其中求出垂线段的长（即斜线上的点到面的距离）既是关键又是难点，为此可用三棱锥的体积自等来求垂线段的长。 例2 （ 如图2） 长方体ABCD-A 1B 1C 1D 1 , AB=3 ,BC=2, A 1A= 4 ，求AB 与面 AB 1C 1D 所成的角。 解：设点 B 到AB 1C 1D 的距离为h, ∵V B ﹣AB 1C 1=V A ﹣BB 1C 1∴1／3 S △AB 1C 1·h= 1／3 S △BB 1C 1·AB ，易得h=12／5 设AB 与 面 A B 1C 1D 所成的角为θ,则sin θ=h ／AB=4／5

2020年高考文科数学《线面角》

1.如图，在四棱锥中，底面为平行四边形，为等边三角形，平面 平面，，，， （Ⅰ）设分别为的中点，求证：平面； （Ⅱ）求证：平面； （Ⅲ）求直线与平面所成角的正弦值. 1.解析 （Ⅰ）连接，易知，.又由， 故，又因为平面，平面，所以平面. （Ⅱ）取棱的中点，连接.依题意，得，又因为平面平面，平面平面，所以平面，又平面，故. 又已知，，所以平面. （Ⅲ）连接，由（Ⅱ）中平面，可知为直线与平面所成的角， 因为为等边三角形，且为的中点，所以 又， 故在中，. 所以，直线与平面 2.如图，已知三棱柱，平面平面,， 分别是AC ，A 1B 1的中点. （1）证明：； （2）求直线EF 与平面A 1BC 所成角的余弦值. P ABCD -ABCD PCD PAC ⊥PCD PA CD ⊥2CD =3AD =G H ，PB AC ，GH ∥PAD PA ⊥PCD AD PAC BD AC BD H =BH DH =BG PG =GH PD ∥GH ?PAD PD ?PAD GH ∥PAD PC N DN DN PC ⊥PAC ⊥PCD PAC PCD PC =DN ⊥PAC PA ?PAC DN PA ⊥PA CD ⊥CD DN D =PA ⊥PCD AN DN ⊥PAC DAN ∠AD PAC PCD △2CD =N PC DN =DN AN ⊥Rt AND △sin 3 DN DAN AD ∠= =AD PAC 111ABC A B C -11A ACC ⊥ABC 90ABC ∠=?11 30,,,BAC A A AC AC E F ∠=?==EF BC ⊥

2.（I ）连接A 1E ，因为A 1A =A 1C ，E 是AC 的中点，所以A 1E ⊥A C. 又平面A 1ACC 1⊥平面ABC ，A 1E 平面A 1ACC 1， 平面A 1ACC 1∩平面ABC =AC ， 所以，A 1E ⊥平面ABC ，则A 1E ⊥BC . 又因为A 1F ∥AB ，∠ABC =90°，故BC ⊥A 1F . 所以BC ⊥平面A 1EF . 因此EF ⊥B C. （Ⅱ）取BC 中点G ，连接EG ，GF ，则EGFA 1是平行四边形． 由于A 1E ⊥平面ABC ，故AE 1⊥EG ，所以平行四边形EGFA 1为矩形． 由（I ）得BC ⊥平面EGFA 1，则平面A 1BC ⊥平面EGFA 1， 所以EF 在平面A 1BC 上的射影在直线A 1G 上. 连接A 1G 交EF 于O ，则∠EOG 是直线EF 与平面A 1BC 所成的角（或其补角）. 不妨设AC =4，则在Rt △A 1EG 中，A 1E ，EG 由于O 为A 1G 的中点，故， ?12A G EO OG == =

高中立体几何专题：线面角与线线角

线面角与线线角 1、异面直线所成的角：（1）范围：(0,]2 π θ∈；（2）求法； 2、直线和平面所成的角：（1）定义：（2）范围：[0,90]o o ；（3）求法； 【典型例题】 例1：（1）在正方体1111ABCD A B C D -中，下列几种说法正确的是 （ ） A 、11AC AD ⊥ B 、11D C AB ⊥ C 、1AC 与DC 成45o 角 D 、11AC 与1B C 成60o 角 答案：D 。解析：A 1C 1与AD 成45°，D 1C 1与AB 平行，AC 1与DC 。 （2）在正方体AC 1中，过它的任意两条棱作平面，则能作得与A 1B 成300角的平面的个数为 （ ） A 、2个 B 、4个 C 、6个 D 、8个 答案：B 。解析：平面A 1ACC 1，平面BB 1D 1D ，平面ABC 1D 1，平面A 1D 1CC 1。 （3）正六棱柱ABCDEF －A 1B 1C 1D 1E 1F 1底面边长是1 面对角线E 1D 与BC 1所成的角是 （ ） A ．90o B ．60o C ．45o D ．30o 答案：B 。解析将BC 1平移到E 1F 即可。 （4）在空间四边形ABCD 中，AB ⊥CD ，BC ⊥DA ，那么对角线AC 与BD 的位置关系是 。 答案：AC ⊥BD 。解析：过A 作AH ⊥平面BCD ，垂足为H ，因为CD ⊥AB ，BC ⊥AD ，所以CD ⊥BH ，BC ⊥DH ，故H 为△BCD 的垂心，从而BD ⊥CH ，可得BD ⊥AC 。 （5）点AB 到平面α距离距离分别为12，20，若斜线AB 与α成030的角，则AB 的长等于__ ___. 答案：16或64。解析：分A 、B 在平面α的同侧和异侧进行讨论。 例3： 如图, 四棱锥P-ABCD 的底面是AB=2, BC =2的矩形, 侧面PAB 是等边三角形, 且侧面 PAB ⊥底面ABCD. (Ⅰ) 证明:BC ⊥侧面PAB; (Ⅱ) 证明: 侧面PAD ⊥侧面PAB; (Ⅲ) 求侧棱PC 与底面ABCD 所成角的大小; 答案： (Ⅰ)证: ∵侧面PAB ⊥底面ABCD, 且侧面PAB 与底面ABCD 的交线是AB, 在矩形ABCD 中, BC ⊥AB ，.∴BC ⊥侧面PAB. (Ⅱ)证: 在矩形ABCD 中, AD ∥BC, BC ⊥侧面PAB, ∴AD ⊥侧面PAB. 又AD ?平面PAD, ∴侧面PAD ⊥侧面PAB. (Ⅲ)解: 在侧面PAB 内, 过点P 做PE ⊥AB, 垂足为E, 连结EC, ∵侧面PAB 与底面ABCD 的交线是AB, PE ⊥AB, ∴PE ⊥底面ABCD. 于是EC 为PC 在底面ABCD 内的射影. A B C D P