基于WKB近似的一维势阱量子化条件推导

能量量子化

17．1 能量量子化 高二物理组韦瑜教材分析、学情分析 本节由黑体和黑体辐射、黑体辐射的实验规律和能量子三部分内容组成。对黑体辐射的研究及由此引发的“紫外灾难”是19世纪初物理学天空中的“第三朵乌云”，然而正是在拨开“第二朵乌云”的过程中，物理学终于迎来了量子物理的曙光。本节的重点是对黑体辐射能量在不同温度下与波长关系的研究，难点是如何让学生理解能量量子化假说。对这部分内容，教材是按物理学史的发展展开的，目的是使学生能从前辈大师的工作中体会科学探究的真实过程。 教学目标 （一）知识与技能 1．了解什么是热辐射及热辐射的特性，了解黑体与黑体辐射 2．了解黑体辐射的实验规律，了解黑体热辐射的强度与波长的关系 3．了解能量子的概念 （二）过程与方法 了解微观世界中的量子化现象。比较宏观物体和微观粒子的能量变化特点。体会量子论的建立深化了人们对于物质世界的认识。 （三）情感、态度与价值观 领略自然界的奇妙与和谐，发展对科学的好奇心与求知欲，乐于探究自然界的奥秘，能体验探索自然规律的艰辛与喜悦。 教学重点 能量子的概念 教学难点 黑体辐射的实验规律 教学方法 教师启发、引导，学生讨论、交流。 教学用具： 投影片，多媒体辅助教学设备 课时安排 1 课时

教学过程 （一）引入新课 教师：介绍能量量子化发现的背景：（多媒体投影，见课件。） 19世纪末页，牛顿定律在各个领域里都取得了很大的成功：在机械运动方面不用说，在分子物理方面，成功地解释了温度、压强、气体的内能。在电磁学方面，建立了一个能推断一切电磁现象的Maxwell方程。另外还找到了力、电、光、声----等都遵循的规律---能量转化与守恒定律。当时许多物理学家都沉醉于这些成绩和胜利之中。他们认为物理学已经发展到头了。 1900年，在英国皇家学会的新年庆祝会上，著名物理学家开尔文作了展望新世纪的发言：“科学的大厦已经基本完成，后辈的物理学家只要做一些零碎的修补工作就行了。” 也就是说：物理学已经没有什么新东西了，后一辈只要把做过的实验再做一做，在实验数据的小数点后面在加几位罢了！ 但开尔文毕竟是一位重视现实和有眼力的科学家，就在上面提到的文章中他还讲到： “但是，在物理学晴朗天空的远处，还有两朵令人不安的乌云，----” 这两朵乌云是指什么呢？ 一朵与黑体辐射有关，另一朵与迈克尔逊实验有关。 然而，事隔不到一年（1900年底），就从第一朵乌云中降生了量子论，紧接着（1905年）从第二朵乌云中降生了相对论。经典物理学的大厦被彻底动摇，物理学发展到了一个更为辽阔的领域。正可谓“山重水复疑无路，柳暗花明又一村”。 点出课题：我们这节课就来体验物理学新纪元的到来――能量量子化的发现（二）进行新课 1．黑体与黑体辐射 教师：在了解什么是黑体与黑体辐射之前，请同学们先阅读教材，了解一下什么是热辐射。 学生：阅读教材关于热辐射的描述。 教师：通过课件展示，加深学生对热辐射的理解。并通过课件展示，使学生进一步了解热辐射的特点，为黑体概念的提出准备知识。 （1）热辐射现象

量子阱原理及应用

光子学原理课程期末论文 ——量子阱原理及其应用 信息科学与技术学院 08电子信息工程 杨晗 23120082203807

题目：量子阱原理及其应用 作者：杨晗 23120082203807 摘要：随着半导体量子阱材料的发展,量子阱器件广泛应用于各种领域.本文主 要介绍量子阱的基本特征,重点从量子阱材料、量子阱激光器、量子阱LED、等方面介绍量子阱理论在光电器件方面的发展及其应用。 关键词：量子阱量子约束激光器 量子阱是指由2种不同的半导体材料相间排列形成的、具有明显量子限制效应的电子或空穴的势阱。量子阱的最基本特征是，由于量子阱宽度(只有当阱宽尺度足够小时才能形成量子阱)的限制，导致载流子波函数在一维方向上的局域化。在由2种不同半导体材料薄层交替生长形成的多层结构中，如果势垒层足够厚，以致相邻势阱之间载流子波函数之间耦合很小，则多层结构将形成许多分离的量子阱，称为多量子阱，简单来说，就是由多个势阱构成的量子阱结构为多量子阱，简称为MQW（Multiple Quantum Well），而由一个势阱构成的量子阱结构为单量子阱，简称为SQW（Single Quantum Well）。 一量子阱最基本特征 由于量子阱宽度(只有当阱宽尺度足够小时才能形成量子阱)的限制，导致载流子波函数在一维方向上的局域化。在由2种不同半导体材料薄层交替生长形成的多层结构中，如果势垒层足够厚，以致相邻势阱之间载流子波函数之间耦合很小，则多层结构将形成许多分离的量子阱，称为多量子阱。如果势垒层很薄，相邻阱之间的耦合很强，原来在各量子阱中分立的能级将扩展成能带(微带)，能带的宽度和位置与势阱的深度、宽度及势垒的厚度有关，这样的多层结构称为超晶格。有超晶格特点的结构有时称为耦合的多量子阱。量子肼中的电子态、声子态 和其他元激发过程以及它们之间 的相互作用，与三维体状材料中的 情况有很大差别。在具有二维自由 度的量子阱中，电子和空穴的态密 度与能量的关系为台阶形状。而不 是象三维体材料那样的抛物线形 状[1]。 图1半导体超晶格的层状结构，白圈和灰圈代 表两种材料的原子

半导体超晶格

半导体超晶格 材料的制造、设计是以固体能带结构的量子力学理论为基础的，也 就是说，人为地改变晶体的周期势，做出具有新功能的人工超晶格 结构材料。半导体超晶格材料具有一般半导体材料不能实现的许 多新现象，可以说是超薄膜晶体制备技术，量子物理和材料设计理 论相结合而出现的第三种类的半导体材料。利用这种材料，不仅可 以显著提高场效应晶体管和半导体激光器等的性能，也可以制备 至今还没有的功能更优异的新器件和发现更多的新物理现象，使 半导体器件的设计和制造由原来的“杂质工程”发展到“能带工 程”。因此，半导体超晶格是属于高科技范畴的新型功能材料。 电子亲和势是指元素的气态原子得到一个电子时放出的能量，叫做电子亲和势。（曾用名：电子亲和能EA）单位是kJ/mol或eV。电子亲和势的常用符号恰好同热力学惯用符号相反。热力学上把放出能量取为负值，例如，氟原子F（g）+e→F-（g），△H=-322kJ/mol。而氟的电子亲和势（EA）被定义为322kJ/mol。为此，有人建议元素的电子亲和势是指从它的气态阴离子分离出一个电子所吸收的能量。于是，氟离子F-（g）-e→F（g），△H＝322kJ/mol。两者所用符号就趋于统一。可以认为，原子的电子亲和势在数值上跟它的阴离子的电离能相同。根据电子亲和势数据可以判断原子得失电子的难易。非金属元素一般具有较大的电子亲合势，它比金属元素容易得到电子。电子亲和势由实验测定，但目前还不能精确地测得大多数元素的电子亲和势。元素的电子亲和势变化的一般规律是：在同一周期中，随着原子序数的增大，元素的电子亲和势一般趋于增大，即原子结合电子的倾向增强，或它的阴离子失去电子的能力减弱。在同一族中，元素的电子亲合势没有明显的变化规律。当元素原子的电子排布呈现稳定的s2、p3、p6构型时，EA值趋于减小，甚至ⅡA族和零族元素的EA都是负值，这表明它们结合电子十分困难。在常见氧化物和硫化物中含有-2价阴离子。从O-（g）或S-（g）结合第二个电子而变成O2-（g）或S2-（g）时，要受到明显的斥力，所以这类变化是吸热的。即O-（g）+e→O2-（g），△H＝780kJ/mol；S-（g）+e→S2-（g），△H＝590kJ/mol。这些能量能从形成氧化物或硫化物晶体时放出的晶格能得到补偿。 电子亲和势与原子失去电子需消耗一定的能量正好相反，电子亲和势是指原子获得电子所放出的能量。 元素的一个气态原子在基态时获得一个电子成为气态的负一价离子所放出的能量，称为该元素的第一电子亲和势(First electron affinity)。与此类推，也可得到第二、第三电子亲和 势。第一电子亲和势用符号“E”表示，单位为kJ·mol·L，如： Cl(g) +e → Cl(g)E= +348.7 kJ·mol·L 大多数元素的第一电子亲和势都是正值（放出能量），也有的元素为负值（吸收能量）。这说明这种元素的原子获得电子成为负离子时比较困难，如： O(g) +e → O(g)E= +141 kJ·mol·L O(g) +e → O(g)E= -780 kJ·mol·L 这是因为，负离子获得电子是一个强制过程，很困难须消耗很大能量。

第十二章-量子物理学

第十二章 量子物理学 §12.1 实物粒子的波粒二象性 一、 德布罗意物质波假设 νλ h E h P == h E P h = = νλ 二、 德布罗意物质波假设的实验证明 1、 戴维森——革未实验 2、 电子单缝实验 例1、运动速度等于300K 时均方根速率的氢原子的德布罗意波长是 1.45A 0 。质量M=1Kg ，以速率v=1cm/s 运动的小球的德布罗意波长是 6.63×10-14A 0 。（h=6.63×10-34J.s 、K=1.38×10-23J.K 、m H =1.67×10-27kg ） 解：（1） m k T v 32= 045.13A k Tm h mv h p h ==== λ （2）0191063.6A Mv h p h -?=== λ 例2、若电子的动能等于其静止能量，则其德布罗意波长是康谱 顿波长的几倍？ 解：电子的康谱顿波长为c m h e c =λ，罗意波长为p h = λ 由题知：c v c m c m E k 2 32)1(2020= ?=?=-=γγ c m h v m h p h e e 2 3 2=== γλ，故 3 1= c λλ 三、 德布罗意物质波假设的意义 四、 电子显微镜 例子、若α粒子（电量为２ｅ）在磁感应强度为Ｂ均匀磁场中沿半径为Ｒ的圆形轨道运动，则α粒子的德布罗意波长是:[A] （A ）ｈ／（２ｅＲＢ） ． （B ）ｈ／（ｅＲＢ） ．

（C）１／（２ｅＲＢｈ）．（D）１／（ｅＲＢｈ）．例2、如图所示，一束动量为ｐ的电子，通过缝宽为ａ的狭缝，在距离狭缝为R处放置一荧光屏，屏上衍射图样中央最大的宽度ｄ等于:[D] （A）２ａ2／Ｒ．] （B）２ｈａ／ｐ． （C）２ｈａ／（Ｒｐ）． （D）２Ｒｈ／（ａｐ）．

一维方势阱

2.4 一维方势阱 本节我们要讨论一维方势阱问题。所谓一维方势阱指的是在一维空间中运动的微观粒子，其势能在一定的区间内，为一负值，而在此区间之外为零，即 00,0,(),0,0,,x U x U x a x a ≤?? =-≤≤??≥? （2.76） 其相应的势能曲线如图2.6所示 图2.6 一维方势阱 下面我们就E 大于与小于零的两种情形分别讨论如下： （1）E>0的情形。 此时，描述粒子运动状态的波函数()x φ所满足的定态薛定谔方程为 22220,l l d m E dx φφ== （2.77） 202 22()0,l m d m E U dx φφ=+= （2.78） 22220,r r d m E dx φφ== (2.79) 式中,l m φφ与r φ分别为粒子位于左方区间、势阱区间与右方区间中的波函数。 为方便起见，令 22 12022 22，()。m m k E k E U = =+ （2.80） 则上述三式可改写为 2212 0,l l d k dx φφ== (2.81) 22 22 0,m m d k dx φφ== (2.82) 2212 0,r r d k dx φφ== (2.83) 其解分别为 1 1 (),ik x ik x l x Ae A c φ-'=+ （2.84） 2 2 (),ik x ik x m x Be B c φ-'=+ （2.85）

1 1 (),ik x ik x r x Ce C c φ-'=+ （2.86） 显然，C 必须为零，利用φ及其导数的连续性条件即可求得、 A C '与A 关系为 2222 1222212122()sin ,()()ik a ik a i k k k a A A k k e k k e --'=--+ (2.87) 122122212124,()()ik a ik a ik a k k e C A k k e k k e --=--+ (2.88) 从而求得其反射系数R 与透射系数T 分别为 222 2122222222 12212()sin ,()sin 4k k k a R k k k a k k -=-+ （2.89） 22 12 222222 12212 4,()sin 4k k T k k k a k k -=-+ （2.90） 由此可见，对于方势阱而言，即使是在E>0的情形下，一般而论，其透射系数T 小于1，而反射系数R 则大于零，二者之和也是等于1。 显然，在2(1,2,)k a n n π== 的特定情形下，其透射系数T 等于1。这种透射亦叫共振透射。此时，有 22 022(),m E U a n π+= (2.91) 与之相应的能量为 222 02 ,2n E U ma π=- (2.92) E n 叫做共振能级。当阱深与阱宽一定时，透射系数T 与人射粒子能量E 的关系如图2.7所示。 图2.7 势阱的透射系数T 与入射能量的关系 当粒子能量E 与阱深一定时，有 0min 2 00 4() ,4()E E U T E E U U += ++ (2.93) 又当入射粒子能量与阱宽一定时，透射系数是阱深U 0的函数，且当满足 222 02 ()2n U n E ma π=- (2.94) 时，T =1。 （2）E<0的情形。 此时，粒子的波函数应满足的定态薛定谔方程为 22220,l l d m E dx φφ-= (2.95)

二次量子化

二次量子化 二次量子化又叫正则量子化，是对量子力学的一种新的数学表述。普通的量子力学方法只能处理粒子数守恒的系统。但在相对论量子力学中，粒子可以产生和湮灭，普通量子力学的数学表述方法不再适用。二次量子化通过引入产生算符和湮灭算符处理粒子的产生和湮灭，是建立相对论量子力学和量子场论的必要数学手段。相比普通量子力学表述方式，二次量子化方法能够自然而简洁的处理全同粒子的对称性和反对称性，所以即使在粒子数守恒的非相对论多体问题中，也被广泛应用。 然而，现在的二次量子化理论反映物质埸的特征是不够全面的。其一：只用作为埸的自由度的广义坐标，是一维的无穷多个指标的广义坐标，也就是说尽管是多个指标，它在空间的自由度却仅有一维。无穷多个指标的广义坐标，只分别对应无穷多个光量子，描写它们一维的状态。为了描写物质埸的矢量性，物质埸 的自由度的广义坐标也应该是多维的广义坐标，必须把推广成，对应物质埸在处的振动的动量，对应物质波的几率密度，即传统的二次量子化理论中的态函数。 在各类物理文献（包括科普）中，我们都能经常看到一个术语，即二次量子化，一般指场量子化或从量子力学到量子场论的这个“提升”过程。然而，所谓的二次量子化其实是一个错误的概念，至少是一个应该被摒弃的不恰当的概念，其产生及仍被使用有着一定的历史根源。但这并不仅仅是历史错误被认识后人们懒得改变的习惯用法，否

则也没有特别说明的必要了，而是依然存在于物理文献中的误解，它还在误导着更多的人。 量子场论的产生是这样一个过程。物理学家们首先建立了基于平直时空点粒子的量子力学，以薛定谔方程来描述，然后为了统一量子力学和狭义相对论，或者说为了找到符合狭义相对性原理的量子力学，他们认为有必要“推广”薛定谔方程，从而找到了克莱恩－戈登方程和狄拉克方程等等并认为他们就是“推广”的薛定谔方程，进一步研究发现这些方程的变量并不是描述点粒子的动力学量，而是所谓的场，一类在时空每一点都有取值的函数，对这类场进行量子化最终促成了量子场论—同时满足狭义相对论和量子力学的新理论的诞生。可是把诸如克莱恩－戈登之类的方程看成薛定谔方程的推广是错误的，正是当年人们这一错误认识导致了二次量子化的提出和使用，并且把量子力学称为经典力学的一次量子化。下面我们简单分析一下。 先从经典点粒子力学说起。经典点粒子力学的研究对象是点粒子，点粒子在空间（即位形空间）中的位置由空间坐标表示，其动力学，即其位置随时间的演化由一个或一组动力学方程所描述，方程的变量是坐标及其时间导数。人们又发现点粒子的动力学也可以等价地通过其位置和动量来描述，一个粒子的位置和动量所构成的空间成为该粒子的相空间，粒子在位形空间中的可能轨迹等价于其相空间中的一条曲线。二十世纪初，一些我们现在已经熟知的原因引发了量子力学革命，物理学家们发现微观世界很大程度上不能为经典相空间所描

量子力学(周世勋)课后答案-第一二章

量子力学课后习题详解 第一章 量子理论基础 1.1 由黑体辐射公式导出维恩位移定律：能量密度极大值所对应的波长m λ与温度T 成反比，即 m λ T=b （常量） ； 并近似计算b 的数值，准确到二位有效数字。 解 根据普朗克的黑体辐射公式 dv e c hv d kT hv v v 1 183 3 -?=πρ， （1） 以及 νc =， （2） ||λνρρλd d v =， （3） 有 (),1 18)(| )(| |5 2-?=?===kT hc v v e hc c d c d d dv λνλ λ πλλρλ λλρλ ρρ 这里的λρ的物理意义是黑体内波长介于λ与λ+d λ之间的辐射能量密度。 本题关注的是λ取何值时，λρ取得极大值，因此，就得要求λρ 对λ的一阶导数为零，由此可求得相应的λ的值，记作m λ。但要注意的是，还需要验证λρ对λ的二阶导数在m λ处的取值是否小于零，如果小于零，那么前面求得的m λ就是要求的，具体如下： 01151186=??? ? ? ?? -?+--?=-kT hc kT hc e kT hc e hc d d λλλλλ πλρ

? 0115=-?+ --kT hc e kT hc λλ ? kT hc e kT hc λλ= -- )1(5 如果令x= kT hc λ ，则上述方程为 x e x =--)1(5 这是一个超越方程。首先，易知此方程有解：x=0，但经过验证，此解是平庸的；另外的一个解可以通过逐步近似法或者数值计算法获得：x=4.97，经过验证，此解正是所要求的，这样则有 xk hc T m =λ 把x 以及三个物理常量代入到上式便知 K m T m ??≈-3109.2λ 这便是维恩位移定律。据此，我们知识物体温度升高的话，辐射的能量分布的峰值向较短波长方面移动，这样便会根据热物体（如遥远星体）的发光颜色来判定温度的高低。

一维势垒问题总结

一维势垒中的透射系数 利用传递矩阵方法研究了粒子在一维势垒中运动时的粒子的透射系数,主要研究的是在一个方势垒两个方势垒中透射系数，对以上的透射系数的总结，推出了对于任意势垒中透射系数， 并讨论了透射系数、反射系数与势垒宽度的关系. 一维方势垒 势垒模型 在方势垒中，遇到的问题和 值得注意的地方。在求方势垒波 函数中，首先要知道这是一个什 么样问题，满足什么样的方程， 方程可以写成什么样的形式，在 求解方程中，波函数的形式应该 怎样需要怎样的分段，分段的过程中，特别要强调的边界条件问题。并且验证了概率流密度。 在量子力学中，粒子在势垒附近发生的现象是不一样的，能量E 大于势垒高度0u 的粒子在势垒中有一部分发生反射，而能量小于0u 的粒子也会有部分穿过势垒，这在经典力学中是不会发生的。 下面讨论的是一维散射（即在非束缚态下问题，在无穷远处波函数不趋于零）。重点讨论的是粒子通过势垒的透射和反射，重点在于求出波函数，这就必须求解薛定谔方程，由于)(x U 是与时间无关的，此处是定态薛定谔方程。 定态薛定谔方程通式： ψψψE U m =+?-2 22h 在量子力学里, 必须知道波函数ψ, 因此必须要解薛定谔方程 t i U x m ??=+??-ψ ψψh h 2222 一维散射问题是一个非束缚态问题(()U x 与时间无关, 而E 是正的).因此令 t E i e x t x h -=)(),(ψψ

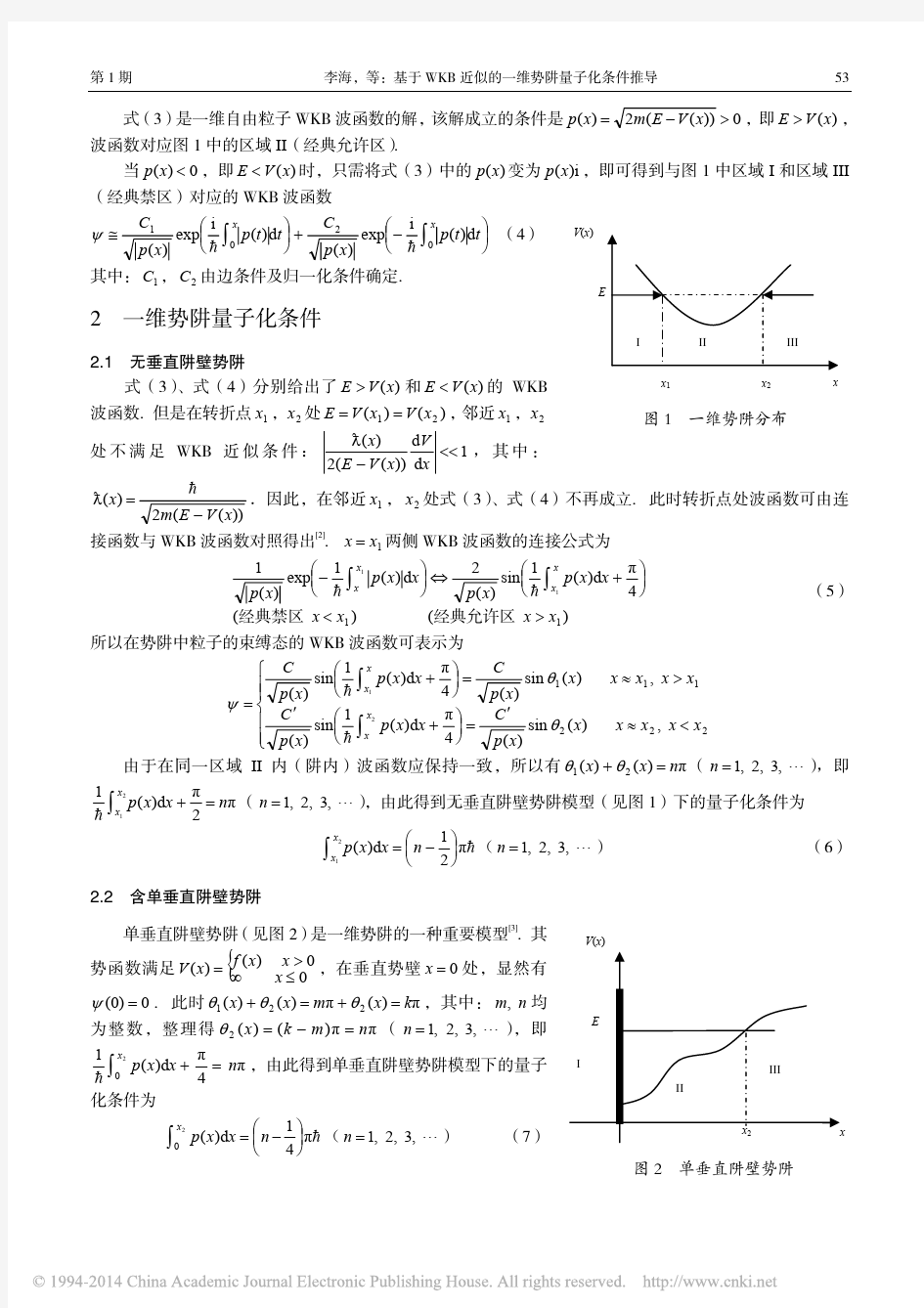
由此得到 ψψψ E U dx d m =+- 2 222h 按照势能()U x 的形式, 方程(2)一般需要分成几个部分求解.将上式改写成如下形式 022 2=+ψψ k dx d ?? ?><<<=. ,0,0; 0,)(0a x x a x u x U 先讨论0u E >的情形 粒子满足薛定谔方程分解为三个区域： ?????? ???>=-<<=+-<=-a x x E x dx d m a x x E x u x dx d m x x E x dx d m ),()(20),()()(20),()(2332 2 222022 2 2112 2 2ψψψψψψψh h h （1） ???? ?????>=+<<=-+<=+a x x mE x dx d a x x u E x dx d x x mE x dx d ,0)(2)(0,0)()()(0,0)(2)(3232220222 12 122ψψψψψψh h 特征方程02=++q pr r 的两个根21,r r 方程 0=+'+''qy y p y 的通解 两个不相等的实根21r r ≠ x r x r e C e C y 2121+= 两个相等的实根21r r = x r e x C C y 1)(21+= 一对共轭复根 βαi r ±=2,1 )sin cos (21x C x C e y x ββα+= 注： 0=+''qy y 的通解:特征方程02=+q r ,当0

WKB近似及在一维势阱量子化条件推导的应用

WKB 近似推导一维势阱量子化条件 摘要：在量子力学里，WKB 近似是一种半经典计算方法，可以用来解析薛定谔方程。WKB 近似的应用非常广泛，特别是量子力学相关问题中。本文通过介绍了WKB 近似，并用其导出了一维势阱量子化条件为例，进一步深入了解WKB 近似法求解方程的步骤和过程。 关键词：WKB 近似，一维势阱，量子化条件，薛定谔方程 引言：WKB 近似全名为温侧-克喇末-布里渊近似法，是以三位物理学家Gregor Went zel 、Hendrix Anthony Kram ers 和Leon Brillouin 命名的。他们于1926年成功的发展和应用于量子力学。经过近百年的发展和改进，WKB 近似已得到完善和普及，应用广泛，如处理谐振子问题、开普勒问题、一维及三维定态微扰问题、分波相角计算问题等。本文主 要讲解的是在势场()x V 变化缓慢并且E —()x V 特别大的条件（即WKB 近似条件）下， 用WKB 近似方法求解一维定态薛定谔方程可以得到WKB 波函数，结合转折点处波函数的渐进行为以及边条件能过导出一维势阱中三种典型模型下的束缚态例子的量子化条件。 1.WKB 近似法的基本思想 若薛定谔方程可以分解为几个常微分方程，并且问题又与经典问题相差不大是，则可以将波函数按幂级数展开，而且只取前面少数几项就能得到到小号的结果。所谓问题与经典问题相差不大，是指在研究体系中，研究的动量与其运动空间尺度大，普朗克常量 作用不大，使量子力学问题退化为经典问题。 2.WKB 近似法的基本步骤 求解一个量子系统的薛定谔方程的基本步骤，由基本思想可以归结为以下五步： 首先将波函数打造为一个一个指数函数；其次是将这些指数函数代入薛定谔方程；然后将指数函数展开为普朗克常量的幂级数的多项式函数；再匹配约化普朗克常量同次幂的项目， 得到一个方程组；最后解析这些方程，得到WKB 近似波函数。 3.WKB 近似波函数 根据上述的基本思想和基本步骤，以一维自由粒子为例，解其WKB 近似波函数的过程如下。 考虑到量子力学与经典力学之间的过度条件：， ()M C M Q .0.→→ 利用准经典近似法（WKB 近似法），对一维自由粒子波函数以 展开，然后求薛定谔方程并取波函数近似解，即可得到WKB 近似波函数。 这一过程的具体步骤为： 对于一维自由粒子波函数??? ??±= i Aex p px ψ可记为()?? ? ??= i ex p x f ψ，将其

量子力学第四版卷一习题答案

第一章 量子力学的诞生 设质量为m 的粒子在谐振子势222 1 )(x m x V ω=中运动，用量子化条件求粒子能量E 的可能取值。 提示：利用 )]([2,,2,1, x V E m p n nh x d p -===?? Λ )(x V 解：能量为E 的粒子在谐振子势中的活动范围为 a x ≤ （1） 其中a 由下式决定：222 1 )(a m x V E a x ω===。 a - 0 a x 由此得 2/2ωm E a = ， （2） a x ±=即为粒子运动的转折点。有量子化条件 h n a m a m dx x a m dx x m E m dx p a a a a ==?=-=-=??? ?+-+-222222222)21(22πωπ ωωω 得ω ωπm n m nh a η22 = = （3） 代入（2），解出 Λη,3,2,1, ==n n E n ω （4） 积分公式： c a u a u a u du u a ++-=-? arcsin 2222 22 2 设粒子限制在长、宽、高分别为c b a ,,的箱内运动，试用量子化条件求粒子能量的可能取值。 解：除了与箱壁碰撞外，粒子在箱内作自由运动。假设粒子与箱壁碰撞不引起内部激发，则碰撞为弹性碰撞。动量大小不改变，仅方向反向。选箱的长、宽、高三个方向为z y x ,,轴方向，把粒子沿z y x ,,轴三个方向的运动分开处理。利用量子化条件，对于x 方向，有 ()?==?Λ,3,2,1, x x x n h n dx p 即 h n a p x x =?2 （a 2：一来一回为一个周期） a h n p x x 2/=∴, 同理可得， b h n p y y 2/=, c h n p z z 2/=, Λ,3,2,1,,=z y x n n n 粒子能量

第二章 一维定态问题

第二章 一维定态问题 一 内容提要 1 几个重要的一维定态问题 [1] 一维无限深势阱 {0 ,00 )(≤≥<<∞ =x a x a x x V ,3,2,122 2 22=μπ= n a n E n ∞≥≤<<π? ??=ψx x a x a x n a x n ,000 s i n 2)( [2] 一维线性谐振子 2221)(x x V μω= ,3,2,1)2 1 (=ω +=n n E n )()(222 1 x H e N x n x n n α-=ψ [其中 ! 2n N n n πα= μω = α ] [3] 定轴转动子 I L H 2??2?= I m E n 22 2 = ),3,2,1,0(21 =π = ψ? m e im n 2 一维定态问题的性质 设)()(* x V x V = [1] 如果)(x ψ是定态S.eq 的解，那么)(x * ψ也是定态S.eq 的解。 [2] 如果)()(x V x V -= 则)(x -ψ也是定态S.eq 的解。 [3] 如果)(x V 是x 的连续函数，那么)(x ψ和)(' x ψ也是连续的； 如果)(x V 为阶梯形方势???><=a x V a x V x V 2 1)(且12V V -有限， 那么)(x ψ和)('x ψ也是连续的； 如果∞→-12V V 时，那么)(x ψ连续而)(' x ψ不连续；

二 例题讲解 1 设粒子处于一维无限深势阱中，{0 ,00 )(≤≥<<∞ =x a x a x x V ， 证明处于能量本征态)(x n ψ的粒子，)6 1(12)(2/2222 π -=-=n a x x a x 讨论 ∞→n 的情况，并与经典力学计算结果比较。 证明：2sin 2)(020 2 a dx a x n x a dx x x x a a n =π=ψ=?? )6 1(124)()(2220 22 2 2 2 2 π-=- ψ=-=-?n a a dx x x x x x x a n 经典情况下，在区域),0(a 中粒子处于dx 范围中的几率为 a dx 则 20a a dx x x a ==? 320 22a a dx x x a ==? 1243)(2222 22a a a x x x x =-=-=- 2 设粒子处于一维无限深势阱中，粒子的波函数为)()(x a Ax x -=ψ，A 为归一化常数。 [1] 求A ；[2] 粒子处于能量本征态a x n a x n π=ψsin 2)(的几率n P 。 解：[1] 由归一化条件 ?? +∞ ∞ -=-=ψa dx x a Ax dx x 0 2 2 1)]([)( 得530 a A = 所以)(30 )(5x a x a x -=ψ [2] )(x ψ用)(x n ψ展开，)()(x c x n n ψ =ψ∑ )c o s 1(15 4)()(3 3π-π =ψψ=? n n dx x x c n n 2662 ])1(1[240n n n n c P --π= = 999.0])1(1[2402 16 1≈--π =P 这表明)(x ψ与)(1x ψ的几率几乎相同。 3设粒子处于一维无限深势阱中的基态)1(=n ，设0=t 时势阱宽突然变为a 2，粒子的波 函数来不及改变，即a x a x x π= ψ=ψsin 2)()0,(1 问 [1] )0,(x ψ是否还是能量本征态？ [2] 粒子处于能量1E 的几率。 解：[1] 加宽后的一维无限深势阱的能量本征值和本征态分别是：

8.3 异质结量子阱及超晶格结构

第八讲 8.3半导体异质结量子阱及超晶格结构

量子阱：能够对电子（空穴）的运动产生某种约束，使其能量量子化的势场。如量子力学中的一维方势阱、有限势阱。 量子阱中的电子在垂直异质结界面方向上其能量是量子化的，而在与异质结界面平行的二维平面内作自由电子运动。因此，把量子阱中的电子称为二维电子气（2DEG）。 （a）双异质结单量子阱 （a） i-GaAs n-Al X Ga3-X As 2--DEG E2 E F E1 △E C （b）调制掺杂异质结界面量子阱 E GA E GB

（一）双异质结间的单量子阱结构 双异质结结构： Al x Ga 1-x As/GaAs /Al x Ga 1-x As，要求GaAs层足够薄。 1、导带量子阱中的电子能态 设势阱的宽度为l ，取垂直于界面的方向为z 轴，势阱中间点为原点，求解薛定谔方程，可得到如下结论：

（一）双异质结间的单量子阱结构 （1）势阱中电子沿 z 轴方向运动受限，在平行于结面的运动是自由的，形成了二维电子气； （2）势阱中电子态的能值分裂为一些分立能级E1，E2…，E i…，对应于电子的束缚态，如图3所示； 图3 双异质结单量子阱中的能级分布

（3）E z<ΔE c 时，电子的波函数在势阱内为 z 的正弦或余弦函数,如图 4 所示；（4）不管 ΔE c 值的大小，至少有一个解存在； （5）势阱深度 ΔE c 越大，阱内的束缚态越多； （6）势阱中的状态密度变为台阶状分布，如图 5 所示。 图 4 束缚态能级与波函数图 5 电子态密度分布

2、价带量子阱中的空穴能态 在Al x Ga1-x As/GaAs/Al x Ga1-x As 双异质结量子阱中，空穴处于价带量子阱中，也在与结面平行的面内形成二维空穴气。 势阱中空穴态的能值分裂为一些分立能级，形成空穴的束缚态能级。由于轻、重空穴有效质量的不同，形成轻重空穴能级混合交叉的分立束缚态能级。 如图 6 所示。

物质量量子化方法

摩尔是一系统的物质的量，该系统中所包含的基本单元数与0.012kg 碳—12的原子数目相等。使用摩尔时应予以指明基本单元，它可以是原子、分子、离子、电子及其他粒子，或是这些粒子的特定组合。 0.012kg 碳—12中所含的原子数目叫做阿伏加德罗常数，符号为A N 。阿伏加德罗常数的近似值为236.0210?/mol ，具体数值是236.022136710?/mol ，这个常数可用很多种不同的方法进行测定。这些方法的理论根据各不相同，但结果却几乎一样差异都在实验方法误差范围之内，这说明阿伏加德罗常数是客观存在的重要数据。 物质量量子化方法 1、洛希密脱的理论计算 1865年，洛希密脱根据气体分子运动论并结合固体密度的实验数据，得出关于A N 的最早可靠估计值231010/A N mol ≈?他的理论计算如下： 洛希密脱根据气体分子运动论的平均自由程公式 从麦克斯韦速率分布函数求得的平均速率 及由气体输运过程得到的粘滞系数 得到 假定固体分子互相紧接着，每个分子占据一个边长为d 的正方体，则1mol 固体占据体积为3 A N d 于是，固体的密度为

洛希密脱的理论计算结果表明阿伏伽德罗常数是一个大得惊人的天文数字。 2、爱因斯坦的贡献 爱因斯坦在1905年和1906年发表的一系列论文中仔细分析了布朗运动，他的分析主要是关于在时间t内微粒的总位移是在很大范围内变化的，而其分量的均方值2x对于悬浮在粘滞系数为n的液体中半径为a的球形微粒来说，则有【1】 （1） 上式称为布朗运动的爱因斯坦公式。推导如下： 设微粒是半径为a的球体，根据斯托克斯定理，它在流体中运动所受粘滞力 （2）根据经典力学定律微粒的运动方程为 （3） F F F表示液体分子由于热运动而产生的对微粒的碰撞力。 其中,, x y z 假设t=0时微粒位于坐标原点, 则x,y,z代表微粒在t时刻的位移, 以x,y,z乘（2）式的3个式子并考虑到 则（1）式可以写为

量子阱半导体激光器的模拟研究分析

量子阱半导体激光器的模拟研究分析 孙涛章双玉陈小霞熊廷文文晋吾刘波吴国阳朱善林郭旭 ( 华中科技大学电子科学与技术系003班武汉430074 ) Simulation of Single Quantum Well Laser Diode Sun Tao Zhang Shuang-yu Chen Xiao-xia Xiong Ting-wen Wen Jing-wu Liu Bo Wu Guo-yang Zhu Shan-lin Guo Xu (Dept of Electronics of Science & Technology, Hua Zhong Univ. of Science & Technology, Wuhan 430074, P.R.China ) Abstract: The principle of single quantum well laser diode（SQW－LD）was reviewed．Discussion was given on the functionality of the gate－way state（quasi-2 dimensional state）which was introduced to describe the transportation of carriers and photons between the separated confinement heterostructure (SCH) and the quantum well．A relative complete set of the equations was presented through a equivalent circuit model ．By means of simulink，which is a functional module of Matlab，a mathematical model for digital analysis of SQW－LD was proposed．The Model i s easy to use．It provides with the advantages of short computation time，real-time supervision and control，convenience for parameter modification．It was used to simulate the opto－electronic behaviors of SQW－LD，such as carrier/photon establishment under step drive current，optical power-drive current relationship，and frequency response to small signal modulation．The results are in good agreement with the reported data．The model can be used for the purpose of device technique improvement and for automatic design and performance simulation of optical fiber networks. Key words: Super lattice Quantum well Single quantum well laser diode (SQW－LD) rate equation Simulation

量子力学(周世勋)课后答案-第一二章

量子力学课后习题详解 第一章 量子理论基础 1.1 由黑体辐射公式导出维恩位移定律：能量密度极大值所对应的波长m λ与温度T 成反比，即 m λ T=b （常量）； 并近似计算b 的数值，准确到二位有效数字。 解 根据普朗克的黑体辐射公式 dv e c hv d kT hv v v 1 183 3 -?=πρ， （1） 以及 λνc =， （2） ||λνρρλd d v =， （3） 有 这里的λρ的物理意义是黑体内波长介于λ与λ+d λ之间的辐射能量密度。 本题关注的是λ取何值时，λρ取得极大值，因此，就得要求λρ 对λ的一阶导数为零，由此可求得相应的λ的值，记作m λ。但要注意的是，还需要验证λρ对λ的二阶导数在m λ处的取值是否小于零，如果小于零，那么前面求得的m λ就是要求的，具体如下： 如果令x=kT hc λ ，则上述方程为 这是一个超越方程。首先，易知此方程有解：x=0，但经过验证，此解是平庸的；另外的一个解可以通过逐步近似法或者数值计算法获得：x=4.97，经过验证，此解正是所要求的，这样则有 把x 以及三个物理常量代入到上式便知 这便是维恩位移定律。据此，我们知识物体温度升高的话，辐射的能量分布的峰值向较短波长方面移动，这样便会根据热物体（如遥远星体）的发光颜色来判定温度的高低。

1.2 在0K 附近，钠的价电子能量约为3eV ，求其德布罗意波长。 解：根据德布罗意波粒二象性的关系，可知 λ h P =。 所考虑的粒子是非相对论性的电子（动能eV c m E e k 621051.0?=<<），满足 e k m p E 22 =， 因此利用非相对论性的电子的能量—动量关系式，有 在这里，利用了 m eV hc ??=-61024.1， eV c m e 621051.0?=。 最后，对 E m h e 2= λ 作一点讨论，从上式可以看出，当粒子的质量越大时，这个粒子的波长就越短，因而这个粒子的波动性较弱，而粒子性较强；同样的，当粒子的动能越大时，这个粒子的波长就越短，因而这个粒子的波动性较弱，而粒子性较强，由于宏观世界的物体质量普遍很大，因而波动性极弱，显现出来的都是粒子性，这种波粒二象性，从某种子意义来说，只有在微观世界才能显现。 自然单位制： 在粒子物理学中，利用三个普适常数（光速c ，约化普朗克常数,玻耳兹曼常数 k ）来减少独立的基本物理量的个数，从而把独立的量纲减少到只有一种（能量量纲，常用单位eV ）。例：1nm=5.07/keV ，1fm=5.07/GeV ， 电子质量m=0.51MeV . 核子（氢原子）质量M=938MeV ，温度5 18.610K eV -=?.

量子阱原理及应用

光子学原理课程期末论文——量子阱原理及其应用 信息科学与技术学院 08电子信息工程 杨晗 23120082203807

题目：量子阱原理及其应用 作者：杨晗23120082203807 摘要：随着半导体量子阱材料的发展,量子阱器件广泛应用于各种领域.本文主要 介绍量子阱的基本特征,重点从量子阱材料、量子阱激光器、量子阱LED、等方面介绍量子阱理论在光电器件方面的发展及其应用。 关键词：量子阱量子约束激光器 量子阱是指由2种不同的半导体材料相间排列形成的、具有明显量子限制效应的电子或空穴的势阱。量子阱的最基本特征是，由于量子阱宽度(只有当阱宽尺度足够小时才能形成量子阱)的限制，导致载流子波函数在一维方向上的局域化。在由2种不同半导体材料薄层交替生长形成的多层结构中，如果势垒层足够厚，以致相邻势阱之间载流子波函数之间耦合很小，则多层结构将形成许多分离的量子阱，称为多量子阱，简单来说，就是由多个势阱构成的量子阱结构为多量子阱，简称为MQW（Multiple Quantum Well），而由一个势阱构成的量子阱结构为单量子阱，简称为SQW（Single Quantum Well）。 一量子阱最基本特征 由于量子阱宽度(只有当阱宽尺度足够小时才能形成量子阱)的限制，导致载流子波函数在一维方向上的局域化。在由2种不同半导体材料薄层交替生长形成的多层结构中，如果势垒层足够厚，以致相邻势阱之间载流子波函数之间耦合很小，则多层结构将形成许多分离的量子阱，称为多量子阱。如果势垒层很薄，相邻阱之间的耦合很强，原来在各量子阱中分立的能级将扩展成能带(微带)，能带的宽度和位置与势阱的深度、宽度及势垒的厚度有关，这样的多层结构称为超晶格。有超晶格特点的结构有时称为耦合的多量子阱。量子肼中的电子态、声子态 和其他元激发过程以及它们之间 的相互作用，与三维体状材料中的 情况有很大差别。在具有二维自由 度的量子阱中，电子和空穴的态密 度与能量的关系为台阶形状。而不 是象三维体材料那样的抛物线形 状[1]。 图1半导体超晶格的层状结构，白圈和灰圈代 表两种材料的原子

量子力学课后答案

=，量子力学习题及解答 第一章 量子理论基础 1．1 由黑体辐射公式导出维恩位移定律：能量密度极大值所对应的波长m λ与温度T 成反比，即 m λ T=b （常量）； 并近似计算b 的数值，准确到二位有效数字。 解 根据普朗克的黑体辐射公式 dv e c hv d kT hv v v 1 1833 -? =πρ， （1） 以及 c v =λ， （2） λρρd dv v v -=， （3） 有 ,1 18)()(5-?=?=?? ? ??-=-=kT hc v v e hc c d c d d dv λλλ πλλρλλ λρλρ ρ 这里的λρ的物理意义是黑体内波长介于λ与λ+d λ之间的辐射能量密度。 本题关注的是λ取何值时，λρ取得极大值，因此，就得要求λρ 对λ的一阶导数为零，由此可求得相应的λ的值，记作m λ。但要注意的是，还需要验证λρ对λ的二阶导数在m λ处的取值是否小于零，如果小于零，那么前面求得的m λ就是要求的，具体如下： 011511 86' =???? ? ?? -?+--?=-kT hc kT hc e kT hc e hc λλλλλπρ ? 011 5=-?+--kT hc e kT hc λλ

? kT hc e kT hc λλ= -- )1(5 如果令x= kT hc λ ，则上述方程为 x e x =--)1(5 这是一个超越方程。首先，易知此方程有解：x=0，但经过验证，此解是平庸的；另外的一个解可以通过逐步近似法或者数值计算法获得：x=，经过验证，此解正是所要求的，这样则有 xk hc T m = λ 把x 以及三个物理常量代入到上式便知 K m T m ??=-3109.2λ 这便是维恩位移定律。据此，我们知识物体温度升高的话，辐射的能量分布的峰值向较短波长方面移动，这样便会根据热物体（如遥远星体）的发光颜色来判定温度的高低。 1．2 在0K 附近，钠的价电子能量约为3eV ，求其德布罗意波长。 解 根据德布罗意波粒二象性的关系，可知 E=hv ， λ h P = 如果所考虑的粒子是非相对论性的电子（2 c E e μ<<动），那么 e p E μ22 = 如果我们考察的是相对性的光子，那么 E=pc 注意到本题所考虑的钠的价电子的动能仅为3eV ，远远小于电子的质量与光速平方的乘积，即eV 6 1051.0?，因此利用非相对论性的电子的能量——动量关系式，这样，便有 p h = λ nm m m E c hc E h e e 71.01071.031051.021024.12296 6 2=?=????= ==--μμ