当前位置：搜档网 › 运筹学答案(熊伟)下

运筹学答案(熊伟)下

习题七

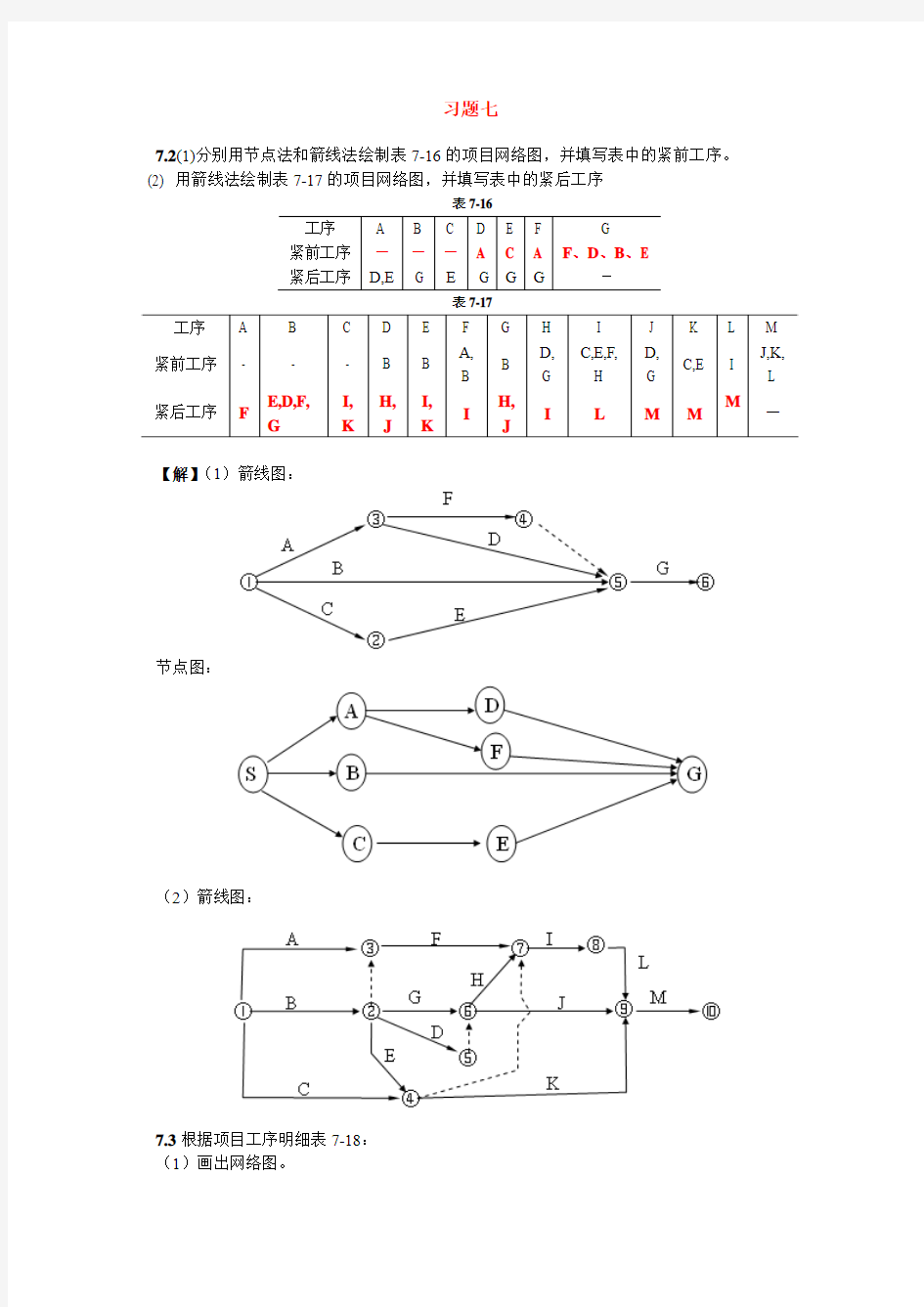
7.2(1)分别用节点法和箭线法绘制表7-16的项目网络图，并填写表中的紧前工序。

(2) 用箭线法绘制表7-17的项目网络图，并填写表中的紧后工序

表7-16

表7-17

【解】（1）箭线图：

节点图：

（2）箭线图：

7.3根据项目工序明细表7-18：

（1）画出网络图。

（2）计算工序的最早开始、最迟开始时间和总时差。

（3）找出关键路线和关键工序。

表7-18

【解】(1)网络图

(2)网络参数

(3)关键路线：①→②→③→④→⑤→⑥→⑦；关键工序：A、C、D、G；完工期：48周。

7.4 表7-19给出了项目的工序明细表。

表7-19

（2）在网络图上求工序的最早开始、最迟开始时间。

（3）用表格表示工序的最早最迟开始和完成时间、总时差和自由时差。

（4）找出所有关键路线及对应的关键工序。

（5）求项目的完工期。

【解】(1)网络图

（2）工序最早开始、最迟开始时间

（3）用表格表示工序的最早最迟开始和完成时间、总时差和自由时差

工序t T ES T EF T LS T LF 总时差S 自由时差F

A 8 0 89 1790

B 5 0 50 500

C 7 0 77 700

D 12 8 2017 2999

E 8 5 13 5 1300

F 17 7 247 2400

G 16 13 2913 2900

H 8 29 3729 3700

I 14 13 2733 472020

J 5 13 1819 246 6

K 10 37 4737 4700

L 23 24 4724 4700

M 15 47 6247 6200

N 12 47 5950 623 3

(4)关键路线及对应的关键工序

关键路线有两条，第一条：①→②→⑤→⑥→⑦→○11→○12；关键工序：B,E,G,H,K,M 第二条：①→④→⑧→⑨→○11→○12；关键工序：C,F,L,M

（5）项目的完工期为62天。

7.5已知项目各工序的三种估计时间如表7-20所示。

求：表7-20

（1）绘制网络图并计算各工序的期望时间和方差。

（2）关键工序和关键路线。（3）项目完工时间的期望值。

（4）假设完工期服从正态分布，项目在56小时内完工的概率是多少。

（5）使完工的概率为0.98，最少需要多长时间。【解】（1）网络图

(2)(3) 项目完工时间的期望值：10.17+14.83+17.17+11.83＝54(小时)

完工期的方差为0.25+0.25+0.6944+0.6944＝1.8889

1.37437σ

(4)X 0=56，05654(1.45520.9271.37437n n X μ

σ??--??Φ=Φ

? ?????

Φ＝）＝

56天内完工的概率为0.927

(5) p=0.98，0{)()0.98, 2.05p X X Z Z ≤=Φ==

0 2.05 1.37445456.82X Z σμ+=?+=＝

要使完工期的概率达到0.98，则至少需要56.82小时。

7.6 表7-21给出了工序的正常、应急的时间和成本。

表7-21

（1）绘制项目网络图，按正常时间计算完成项目的总成本和工期。

（2）按应急时间计算完成项目的总成本和工期。

（3）按应急时间的项目完工期，调整计划使总成本最低。

（4）已知项目缩短1天额外获得奖金4万元，减少间接费用2.5万元，求总成本最低的项目完工期。

(1) 正常时间项目网络图

项目网络图

总成本为435，工期为64。

(2)应急时间项目网络图

总成本为560，工期为51。

(3)应急时间调整

工序C、F按正常时间施工，总成本为560-9-15＝536，完工期为51。

(4) 总成本最低的项目完工期

工序A、E分别缩短3天，总成本为435+15+12-6.5×7＝416.5，完工期为57。

7.7继续讨论表7-21。假设各工序在正常时间条件下需要的人员数分别为9、12、12、6、8、17、14人。

（1）画出时间坐标网络图

（2）按正常时间计算项目完工期，按期完工需要多少人。

（3）保证按期完工，怎样采取应急措施，使总成本最小又使得总人数最少，对计划进行系统优化分析。

【解】（1）正常时间的时间坐标网络图

(2) 按正常时间调整非关键工序的开工时间

(3)略，参看教材。

7.8用WinQSB 软件求解7.5。 7.9用WinQSB 软件求解7.6。

习题八

8.1 在设备负荷分配问题中，n =10，a =0.7，b =0.85，g =15，h =10，期初有设备1000台。试利用公式(8.7)确定10期的设备最优负荷方案。【解】将教材中a 的下标i 去掉。

由公式1

0()n t n t

i i i g h

a a g

b a ---==-≤≤-∑∑得

(g -h )/g (b -a )＝0.2222，a 0＋a 1＋a 2＝1+0.7＋0.49＝2.19＜2.222＜a 0+a 1＋a 2＋a 3＝2.533，n －t

－1＝2，t =7，则1~6年低负荷运行，7~10年为高负荷运行。各年年初投入设备数如下表。

年份

1 2 3 4 5 6 7 8 9 10 设备台数 1000 850 723 614 522 444 377 264 184.8 129 8.2如图8－4，求A 到F 的最短路线及最短距离。【解】A 到F 的最短距离为13；最短路线 A→ B2→ C3 → D2 → E2 → F 及A→C 2 → D2 → E2 → F

8.3求解下列非线性规划

(1) 123123max 0,1,2,3j Z x x x x x x C x j =++=???

≥=?? (2) 22

123

123123min ,,0Z x x x x x x C

x x x =++++=??

≥? （3） 2123

123123m a x 2310

,,0

Z x x x x x x x x x =++++=??

≥?

(4) 123

123max 42100,1,2,3j Z x x x x x x x j =++=???

≥=?? (5) 123

123max 24100,1,2,3j Z x x x x x x x j =++≤???

≥=?? （6）22

1123

123123max 228

,,0

Z x x x x x x x x x x =+++++=??

≥?

【解】（1）设s 3=x 3 , s 3+x 2=s 2，s 2+x 1=s 1=C 则有 x 3= s 3 ，0≤x 2≤s 2，0≤x 1≤s 1=C 用逆推法，从后向前依次有

k ＝3， 33

3333()max()x s f s x s === 及最优解 x 3*=s 3

k ＝2，22

22233222222000()max [()max [()]max (,)x s x s x s f s x f x x s x h s x ≤≤≤≤≤≤==-=

由

2222221

20,2

h s x x s x ?=-=?则＝ 22

2<0,h x ??＝－故 2212x s =为极大值点。所以 222

22222111()244

f s s s s =-= 及最优解x 2*=s 2

k =1时， 1111112

111221*********()max[()]max ()max (,)4

x s x s x s f s x f s x s x h s x ≤≤≤≤≤≤==-=，

由22

1111111(43)04

h s s x x x ?=-+=?，得*1113x s =

故23

111111111()()12327

f s s s s s =-= 已知知x 1 + x 2+ x 3 = C ，因而按计算的顺序推算，可得各阶段的最优决策和最优解如下

113x C =，311()27

f C c =

由s 2=s 1－x 1*=2C/3，*

222211

,()39x C f s C =

= 由s 3=s 2－x 2*=C/3，*

33311,()33

x C f s C ==

最优解为：

1111(,,);33327

T X C C C z C ==

【解】（2）设s 3=x 3 , s 3+x 2=s 2，s 2+x 1=s 1=C

则有 x 3= s 3 ，0≤x 2≤s 2，0≤x 1≤s 1=C 用逆推法，从后向前依次有

k ＝3， 2

333333

()min()x s f s x s === 及最优解 x 3*=s 3

k ＝2，22

222

22233222222022

00()min [()min [()]min (,)x s x s x s f s x f x x s x h s x ≤≤≤≤≤≤=+=+-=

由2222221

420,2

h s x x s x ?=-=?则＝

22x h ??=4>0,故 x 2=221

s 为极小值点。因而有2*2222211

(),22

f s s x s ==

k ＝1时， 1111211111111

001()min [()min (,)2

x s x s f s x s x h s x ≤≤≤≤=+-= 由1111

10h s x x ?=-+=?知 *

1111111,()2x s f s s =-=-

得到最优解

(1,1/2,1/2);2

T X C z C =-=-

【解】(3) 设s 3=x 3 , s 3+x 2=s 2，s 2+x 1=s 1=10 则有 x 3= s 3 ，0≤x 2≤s 2，0≤x 1≤s 1=10 用逆推法，从后向前依次有

k ＝3时，33

3333()max()x s f s x s === 及最优解 x 3=s 3

k ＝2时，22

2222222200()max [3()]max (,)x s x s f s x s x h s x ≤≤≤≤=+-=

2222223

32202

h s x x s x ?=-+==-+?时而 22222

2320,2

h x s x ?=>=-+?故不是一个极大值点。讨论端点：当 x 2=0时2

222()f s s ＝, x 2= s 2时222()3f s s =

如果s 2>3

时, 2

222()f s s =

k ＝1时，11

1111111100()max[2()]max (,)x s x s f s x s x h s x ≤≤≤≤=+-=

11111

22201h s x x s x ?=-+==-+?时 21122

20,1h x s x ?=>=-+?故不是一个极大值点同理有, x 1=0, f 1（s 1）= s 12= 100，x 1= s 1, f 1（s 1）= 2s 1= 20 (舍去) 得到最优解

(0,0,10);100X z ==

【解】(4) 设s 3=x 3 ,2s 3+4x 2=s 2，s 2+x 1=s 1=10 则有 x 3= s 3 ，0≤x 2≤s 2/4，0≤x 1≤s 1=10 用逆推法，从后向前依次有 k ＝1，

3333()max()x s f s x s ===及最优解 x 3*=s 3

k ＝2， 2222222222220404

()m a x [(2)

m a x (,)

x s x s f s x s x h s x

≤≤≤≤=

-= 由22x h ??=2

1s 2-4x 2=0,则 x 2=81

s 2

40h x ?=-

22()32

s f s = 及最优解x 2*=s 2/8

k ＝1， 1111

211111111001

()max[

()]max (,)32x s x s f s x s x h s x ≤≤≤≤=-= 22*1111111

111(43)0,323

h s s x x x s x ?=-+==?，故 31111()216f s s = 得到最优解

(10/3,5/6,5/3);125/27T X z ==

【解】(5) 按问题中变量的个数分为三个阶段s 1 ，s 2 ，s 3 ，且s 3≤10，x 1，x 2，x 3为各阶段

的决策变量，各阶段指标函数相乘。

设s 1=2x 1 , s 1+4x 2=s 2，s 2+x 3=s 3≤10，则有 x 1= s 1/2 ，0≤x 2≤s 2/4，0≤x 3≤s 3=10 用顺推法，从前向后依次有 k ＝1， 111

111/2

()max ()2

x s s f s x ===

及最优化解 x 1*=s 1/2 k ＝2， 2222222222220/40/4

()m a x [(4)

m a x (,

)

x s x s f s x s x h s x ≤≤≤≤=

-= 由22221402

h s x x ?=-=?,则 *

2218x s =

40h x ?=-

233333333001

()max [

()]max (,)32x s x s f s x s x h s x ≤≤≤≤=-= 由22*

3333333311(43)0,323

h s s x x x s x ?=

-+==?

故3

3331()216

f s s =

，由于s 3≤10，则s 3=10时取最大值，x 3＝10/3，s 2=s 3－x 3＝20/3，x 2＝5/6，s 1=s 2－4x 2＝10/3，x 1＝5/3

得到最优解

(5/3,5/6,10/3);125/27T X z ==

【解】（6）设s 1=x 1, s 1+x 2=s 2，s 2+x 3=s 3=8

k ＝1，11

111111()max(2)2x s f s x x s s ==+=+ 及最优化解 x 1*=s 1

k ＝2，22

222222222200()max [2()2()]max (,)x s x s f s x s x s x h s x ≤≤≤≤=+-+-=

2222622,h x s x ?=--?22

60h x ?=>? x 2*=0时，f 2（s 2）=s 22+2s 2, x 2*= s 2时，f 2（s 2）=2s 22

故 22

22222()max{2,2}f s s s s =+

k ＝3，

①当x 2*=0时， 2

3333333333033

033

()max [()2()]max (,)x s x s f s x s x s x h s x ≤≤≤≤=+-+-= 同样得x 3*=0时

，f 3（s 3）=s 32+2s 3

x 3*=s 3时，f 3（s 3）=s 3 所以， f 3（s 3）= s 32+2s 3=80 ②当x 2*= s 2时，f 3（s 3）=3

30max s x ≤≤[x 3+2（s 3-x 3）2] 同样得x 3*=0时

，f 3（s 3）=2s 32 =128

x 3*=s 3时，f 3（s 3）=s 3 =8 所以， f 3（s 3）= 2s 32=128 最优解为

(0,8,0);128X z ==

8.4用动态规划求解下列线性规划问题。

12121212max 242624,0

Z x x x x x x x x =++≤??≤??

≤??≥?

【解】设s 2=x 2 ,s 2+2x 1=s 1≤6

则有 0≤x 2=s 2≤4，0≤x 1≤s 1/2 用逆推法，从后向前依次有 222()4f s s =及最优解 x 2*=s 2

111111122110/2

0/2

()m a x [2()]

m a x [46]

x s x s f s x f s s x ≤≤≤≤=

+=- 由 s 2=s 1－2x 1≤4， s 1≤6，取s 1＝6，

111110/2

()max [246]x s f s x ≤≤=-

又1≤x 1≤2，取x 1＝1，11()18f s =

最优解

(1,4);18T X z ==

8.5 10吨集装箱最多只能装9吨，现有3种货物供装载，每种货物的单位重量及相应单位价值如表8.24所示。应该如何装载货物使总价值最大。

i 123

123123m a x 3452349

,,0

z x x x x x x x x x =++++≤??

≥?且为整数

利用背包问题的前向动态规划计算，建立动态规划模型。由于决策变量离散型值，所以

可用列表法求解。当R=1时，

1210/2

()max (3)x s f s x ≤≤=。计算结果如下：

当R=2时，f 2（s 3）=4

/210s x ≤≤[4x 2+f 1（s 3-3x 2）]

当R=3时，f 3（9）=2

30max ≤≤x [5x 3+f 2（9-4x 3）] （x 3为整数）=2

20max ≤≤x [f 2（9），5+f 2（5），

10+f 2（1）]=max[13，12，10]=13

8.6 有一辆货车载重量为10吨，用来装载货物A 、B 时成本分别为5元/吨和4元/吨。现在已知每吨货物的运价与该货物的重量有如下线性关系：

A ：P 1=10-2x 1 ，

B ：P 2=12-3x 2

其中x 1 、x 2 分别为货物A 、B 的重量。如果要求货物满载，A 和B 各装载多少，才能使总利润最大

【解】将原题改为A ：P 1=15-x 1 ，B ：P 2=18-2x 2 由题意可得各种货物利润函数为

111111

222222()(155)10()(1824)142

g x x x x x g x x x x x =--=-=--=-

原问题的数学模型归结为

11221212max (10)(142)

10,0

z x x x x x x x x =-+-+=??

≥?

最优解：x 1 =6，x 2 =4；z ＝48

8.7 现有一面粉加工厂，每星期上五天班。生产成本和需求量见表8-25。

表8-25

面粉加工没有生产准备成本，每袋面粉的存储费为h k ＝0.5元/袋，按天交货，分别比较下列两种方案的最优性，求成本最小的方案。

（1）星期一早上和星期五晚的存储量为零，不允许缺货，仓库容量为S=40袋；（2）其它条件不变，星期一初存量为8。【解】动态规划求解过程如下：阶段k ：日期，k =1,2,…,6

状态变量s k ：第k 天早上（发货以前）的冷库存量决策变量x k ：第k 天的生产量状态转移方程：s k +1=s k +x k －d k ；

决策允许集合：{}

400,0)(≤-+≤≥=k k k k k k k d x s x x s D 阶段指标： v k (s k ，x k )=c k x k +0.5s k 终端条件：f 6(s 6)=0, s 6=0；递推方程：

{}

)(),(min

)(),(min )(1)

(11)

(k k k k k k k k s k D k x k k k k k k s k D k x k k d x s f x s v s f x s v x f -++=+=+∈++∈

当k =5时，因为s 6=0，有6555550,15,s s x d x s =+-==-

由于s 5≤15，

{}

555515*55

()min 100.51509.5, 15x s f s x s s x s ∈-=+ =-=-

k =4时，5440153015,s s x ≤≤≤+-≤，0有44445s x s -≤≤-30，

{{444444444455()

44()

*444

444()min 120.5()}

min

2.59435}

11.551030,3094354030,0

x D s x D s f s x s f s x s s s x s s s x ∈∈=++=-+?-+≤=-=?-+≤≤=?

k =3时，当0≤s 4≤30时，332530s +x ≤-≤0，得

3332555s x s -≤≤-

有{}

333333()max[0.25]55D s x s x s =-≤≤-

{{{3333

333344()

334()

33()

333

()min

90.5()}

min 90.511.5510}min 2.511797.5}8.5660

55x D s x D s x D s f s x s f s x s s x s s x s ∈∈∈=++=+-+=--+=-+=-取上界：

当30≤s 4≤40时，4330,302540x s +x =≤-≤，有

{}333333()5565D s x s x s =-≤≤-

{{{3333333

(1)333344()

334()

33()

()min

90.5()}

min

90.59435}

min 8.5210},x D s x D s x D s f s x s f s x s s x x ∈∈∈=++=+-+=-+ 取任意值

显然此决策不可行。

当k =2时，由4322030,0252025,s s s x ≤≤≤≤≤+-≤，0x 2的决策允许集合为

{}222222()max[0,20]45D s x s x s =-≤≤-

{{2222

22222()

22()

222

()min

60.56608.5}

min 2.58830}5.5717.5

45x D s x D s f s x s s x s s x s ∈∈=++-=--+=-+=-取上界：

当k =1时，由21102001020s s x ≤≤≤+-≤，，则x 1的决策允许集合为

{}111111()max[0,10]30D s x s x s =-≤≤- {}

{}11111111112()

11()

()min 80.5717.5 5.5min 2.55772.5797.5

x D s x D s f s x s s x s ∈∈=++-=-+=

因为110, 10,s x ==

222322334334454455 10100, 4545, 2025, 5530, 2530, 300, 300, 1515.

s x s s s x x s s s x x s s s x x s =-==-==+-==-==+-==-==+-==-=-

(2)期初存储量s 1=8, 与前面计算相似，x 1=2. Min Z=772.5+2.5x 1-5s 1=737.5 则总成本最小的方案是第二种。

8.8 某企业计划委派10个推销员到4个地区推销产品，每个地区分配1~4个推销员。各地区月收益（单位：10万元）与推销员人数的关系如表8－26所示。

表8-26

企业如何分配4个地区的推销人员使月总收益最大。

【解】设x k 为第k 种货物的运载重量，该问题的静态规划模型为

112233441234max ()()()()80,2,4,6,8

j Z v x v x v x v x

x x x x x =++++++=???=??

利用图表法：

故最优解为12340,0,4x x x x ====

则 max Z=44

8.9 有一个车队总共有车辆100辆，分别送两批货物去A 、B 两地，运到A 地去的利润与车辆数目满足关系100x ，x 为车辆数，车辆抛锚率为30%，运到B 地的利润与车辆数y 关系为80y ，车辆抛锚率为20%，总共往返3轮。请设计使总利润最高的车辆分配方案。【解】动态规划求解过程如下。

阶段k ：共往数k=1,2,3,4，k=1表示第一趟初，k =4表示第三趟末（即第六年初）；状态变量s k ：第k 趟初完好的车辆数（k =1,2,3,4），也是第k －1趟末完好的车辆数，其中s 4表示第三趟末的完好车辆数。

决策变量x k ：第k 年初投入高负荷运行的机器数；状态转移方程：s k +1=0.7x k +0.8(s k －x k ) 决策允许集合：D k (s k )={x k |0≤x k ≤s k } 阶段指标：v k (s k ，x k )=100x k +80(s k －x k ) 终端条件：f 4(s 4)=0 递推方程：

{}

[]{}

11()

10()max

(,)()max 10080()0.70.8()k k k k k

k k k k k k k x D s k k k k k k k x s f s v s x f s x s x f x s x ++∈+≤≤=+=+-++-

f k (x k )表示第k 趟初分配x k 辆车到A 地，到第3趟末的最大总运价为

{}

33333440*333

30()max 10080()()max{2080}100x s x s f s x s x f s x s s x s ≤≤≤≤=+-+ =+==最优

{}

22222330*222

20()max 10080()()max {10160}170x s x s f s x s x f s x s s x s ≤≤≤≤=+-+=+==最优

{}

11111220*111

110()max 10080()()max{3216}219x s x s f s x s x f s x s s x s ≤≤≤≤=+-+=+==最优

因为s 1=100，最大总运价f 1(s 1)=21900元

8.10 系统可靠性问题。一个工作系统由n 个部件串联组成，见图8-5。只要有一个部件失灵，整个系统就不能工作。为提高系统的可靠性，可以增加部件的备用件。例如，用5个部件1并联起来作为一个部件与部件2串联，如果其中一个部件失灵其它4个部件仍能正常工作。由于系统成本（或重量、体积）的限制，应如何选择各个部件的备件数，使整个系统的可靠性最大。

图8-5

假设部件(1,2,,)i i n = 上装有i x 个备用件，该部件正常工作的概率为()i i p x 。设装一个部件i 的备用件的成本为i c ，要求备件的总费用为C 。那么该问题模型为：

max ()

01,2,,n

i i i n i i i j

P p x c x C x i n ===?≤???≥=?∏∑ 并且为整数，（8.8）

同理，如果一个复杂的工作系统由n 个部件并联组成的，只有当n 个部件都失灵，整个系统就不能工作，见图8-6。

图8-6

假设()i i p x 为第i 个部件失灵的概率，为提高系统的可靠性，可以增加部件的备用件。由于系统成本（或重量、体积）的限制，应如何选择各个部件的备件数，使整个系统的可靠性最大。系统的可靠性为1

1()n

i p x =-

∏，则该问题的数学模型归结为

部件1

部件2

……

部件n

min ()

01,2,,n

i i i n

i i i j

P p x c x C x i n ===?≤???≥=?∏∑ 并且为整数，（8.9）利用式(8.8)或（8.9）求解下列问题。

（1）工厂设计的一种电子设备，其中有一系统由三个电子元件串联组成。已知这三个元件的价格和可靠性如表8-27所示，要求在设计中所使用元件的费用不超过200元，试问应如何设计使设备的可靠性达到最大。

表8-27

（2）公司计划在4周内必须采购一批原料，而估计在未来的4周内价格有波动，其浮动价格和概率根据市场调查和预测得出，如表8-28所示，试求在哪一周以什么价格购入，使其采购价格的期望最小，并求出期望值。

表8-28

312123123max (10.05)(10.2)(10.4)403520200,,0x x x Z x x x x x x =---++≤??

≥?并且为整数

最优解X=(1，2，4)；可靠性Z=0.888653，总费用190。（2）

习题九

9.1某蛋糕店有一服务员，顾客到达服从λ=30人/小时的Poisson 分布，当店里只有一个顾客时，平均服务时间为1.5分钟，当店里有2个或2个以上顾客时，平均服务时间缩减至1分钟。两种服务时间均服从负指数分布。试求：（1）此排队系统的状态转移图；（2）稳态下的概率转移平衡方程组；（3）店内有2个顾客的概率；（4）该系统的其它数量指标。【解】（1）此系统为]//[:]1//[FCFS M M ∞∞排队模型，该系统的状态转移图如下：

（2）由转移图可得稳态下的差分方程组如下：

??????

?+=++=++=+=+-n

n n P P P P P P P P P P P )()()(2121223211

12201

10λμμλλμμλλμμλμλ 011P P μλ=∴ 02122P P μμλ= 022133P P μμλ= 01

1P P n n

n -=μμλ （3）已知小时）

（人＝＝小时）（人＝＝小时）（人/6060

/40605.11/3021μμλ= 由

1i i P ∞

==∑得

112

02[1]111n n n P P λμμλμλμ∞

-=-+=??

????=+

??-???

∑

令 1212303301

,404602

λλρρμμ＝＝＝＝＝＝，有

11102

01201

4[1][1]0.4

1112

n n n n P p p p ρ

ρλρρμμ----=+=+=--==

则 212031

0.40.1542

P P ρρ==

??= （4）系统中的平均顾客数（队长期望值）

)(2.1)

5.01(1

4.043)1(1

...)

321(2

22010

320101210

人=-??=-=+++===∑∑∞

=-∞

=ρρρρρρρP P P n nP L n n n n

在队列中等待的平均顾客数（队列长期望值）

)

(4.02

.043

2.11...)...1()1(2

0112222011

人=-?-=--=+++++-=-=-=-∞

=∞=∞=∑∑∑ρρρρρρp L P L P nP P n L n n n

n n n n q

系统中顾客逗留时间

1.2

0.04()30

W λ

=小时系统中顾客等待时间

)(013.030

.0小时==

q L W

9.2某商店每天开10个小时，一天平均有90个顾客到达商店，商店的服务平均速度是每小时服务10个，若假定顾客到达的规律是服从Poisson 分布，商店服务时间服从负指数分布，试求：

（1）在商店前等待服务的顾客平均数。（2）在队长中多于2个人的概率。（3）在商店中平均有顾客的人数。

（4）若希望商店平均顾客只有2人，平均服务速度应提高到多少。【解】此题是属于]//[:]1//[FCFS M M ∞∞系统，其中：

λ=9（个/小时） μ=10(个/小时) μλρ/==9/10

(1) 1.8)1/(2

=-=ρρq L （个）

(2) 729.0)2(3==

>ρN P

(3) 9)1/(=-=ρρL （个） (4) /()2L λμλ=-=

2918

13.522

λλμ++=

==(个/小时)

9.3为开办一个小型理发店，目前只招聘了一个服务员，需要决定等待理发的顾客的位子应设立多少。假设需要理发的顾客到来的规律服从泊松流，平均每4分钟来一个，而理发的时间服从指数分布，平均每3分钟1人。如果要求理发的顾客因没有等待的位子而转向其他理发店的人数占要理发的人数比例为7％时，应该安放几个位子供顾客等待？【解】此题属于]//[:]1//[FCFS N M M ∞模型,依题意知：

λ＝1/4，μ=1/3，μλρ/==3/4 解出L 及q L 的含N 的表达式，令

%7/=q L L 解得N ≈1.67

9.4某服务部平均每小时有4个人到达，平均服务时间为6分钟。到达服从Poisson 流，服务时间为负指数分布。由于场地受限制，服务部最多不能超过3人，求：

（1）服务部没有人到达的概率；（2）服务部的平均人数；

（3）等待服务的平均人数；

（4）顾客在服务部平均花费的时间；（5）顾客平均排队的时间。

【解】依题意，这是]//[:]1//[FCFS N M M ∞排队系统。其中：

N =3，λ=4，μ=10，μλρ/==0.4

（1）1

N 0ρ

-1ρ1+-=P =（1-0.4）/[1-（0.4）4

]=0.6158 （2）5616.0=L （人）

（3）1616.0=q L （人）（4）1404.0=W （小时）（5）0404.0=q W （小时）

9.5某车间有5台机器，每台机器连续运转时间服从负指数分布，平均连续运转时间为15分钟。有一个修理工，每次修理时间服从负指数分布，平均每次12分钟。求该排队系统的数量指标，0P ，q L ，L ，q W ，W 和5P 。

【解】由题意知，每台机器每小时出故障的平均次数服从泊松分布，故该排队系统为]//[:]1//[FCFS m M M ∞系统，其中： λ=1/15，m =5，μ=1/12，μλρ/==0.8

0073.0)!5(!51

500=??????-=-=∑k k k P ρ

766.2)0073.01(15

/112

/115/15=-+-=q L （台）

759.3)1(0=-+=P L L q （台）

43.33)5(=-=

L L W q

q （分钟）

43.451

=+=μ

q W W （分钟）

287.0)0073.0()8.0(!

0!5)!5(!5

5==???? ??-=P m m P μλ

9.6

证明：一个]

//[:]2//[F C F S M M ∞∞的排队系统要比两个]//[:]1//[F C F S M M ∞∞的排队系统优越。试从队长

L 这个指标证明。【证】设]//[:]1//[FCFS M M ∞∞的服务强度为ρ，则]//[:]2//[F

C F S M M ∞∞服务强度为2ρ。则

两个单服务台的系统 ρ

ρρ-=-=1211L 两个服务台的系统 ρρ

ρρ

ρ+-=??++=11)2(12121120P

队长 2

2221211)1(2)2(2ρ

ρρρρρρ-=+-?-??+=L

熊伟编《运筹学》习题十详细解答

习题十 10.1某产品每月用量为50件，每次生产准备成本为40元，存储费为10元/（月·件），求最优生产批量及生产周期。【解】模型4。D=50，A=40，H=10 224050 20()10 /0.4()2210405025200() AD Q H t Q D f HAD ??= ======???=件月元则每隔0.4月生产一次，每次生产量为20件。 10.2某化工厂每年需要甘油100吨，订货的固定成本为100元，甘油单价为7800元/吨，每吨年保管费为32元，求：（1）最优订货批量；（2）年订货次数；（3）总成本。【解】模型4。D=100，A=100，H=32，C=7800 22100100 25()32/4() 22321001007800100780800() AD Q H n D Q f HAD CD ??= =====+=???+?=件次元则（1）最优订货批量为25件；（2）年订货4次；（3）总成本为780800元。 10.3工厂每月需要甲零件3000件，每件零件120元，月存储费率为1.5%，每批订货费为150元，求经济订货批量及订货周期。【解】模型4。D=3000，A=150，H=120×0.015＝1.8，C=120 221503000 707()1.8 /0.24()22 1.815030001203000361272.79() AD Q H t Q D f HAD CD ??= =≈===+=???+?=件月元则经济订货批量为707件，订货周期为0.24月。 10.4某公司预计年销售计算机2000台，每次订货费为500元，存储费为32元/（年·台），缺货费为100元/年·台。试求：（1）提前期为零时的最优订货批量及最大缺货量；（2）提前期为10天时的订货点及最大存储量。【解】模型3。D=2000，A=500，H=32，B=100, L=0.0274(年) 22500200032100 287()32100 AD H B Q H B +??+= =≈台 22500200032 69()10032100AD H S B H B ??= ≈++＝台 1225002000100 218()3232100 AD B Q H H B ??= =≈+台＋ R ＝LD －S ＝0.0274×2000－69＝55－69＝－14（件） (1)最优订货批量为287台，最大缺货量为69台；(2)再订货点为－14台，最大存储量

运筹学

《运筹学》课程教学大纲一、课程基本信息二、课程性质《运筹学》是20世纪40年代开始形成的一门应用性学科。它主要应用定量分析的方法，从系统观念出发，研究如何合理利用有限资源(包括人力、物力、财力、时间和空间等资源)以实现资源的最优配置，提出具有共性、典型意义的优化模型，寻求解决模型的方法，最终形成决策方案。其目的是提高管理者统筹规划、纵揽全局的能力，帮助管理者科学地确定行动方向和行动方案，使之既合乎客观规律，又能获得尽可能好的结果。三、教学目标和任务本课程将通过系统地讲授《运筹学》的基本原理和基本方法、指导学生解题、个人研究与小组讨论相结合的案例分析等环节，培养学生定量分析的基本技能和全局优化的思想，使学生了解最优化计算方法，以及掌握若干类常用的管理运筹学模型，了解管理运筹学模型在解决经济管理领域中相关问题中所起的作用。四、教学要求 1、要求正确理解运筹学方法论，掌握运筹学整体优化思想。 2、要求掌握管理运筹学各分支的基本理论和方法，能根据实际背景抽象出适当的运筹

学模型，熟练掌握各种模型特别是确定性模型的求解方法，并能对求解结果作简单分析。 3、具有初步运用运筹学思想和方法分析、解决实际问题的能力和创新思维与应用能力。五、课程学时安排六、主要内容第一章绪论（2课时）【教学目标】通过本章学习，了解运筹学的性质及特点，发展历史以及学习运筹学的意义。【教学内容】第一节课程导入内容：介绍运筹学简史，运筹学的性质和特点，运筹学的学习方法重点讲授：运筹学简史第二节运筹学模型应用及发展趋势内容：运筹学的模型、应用场景和发展趋势重点讲授：运筹学常用模型【教学重点、难点】运筹学的性质特点和应用，运筹学的未来的发展趋势思考题：

熊伟编《运筹学》习题九详细解答

n 1 1 2 p 习题九 9.1某蛋糕店有一服务员，顾客到达服从 =30人/小时的Poisson 分布，当店里只有一个顾客时，平均服务时间为 1.5分钟，当店里有2个或2个以上顾客时，平均服务时间缩减至 1 分钟。两种服务时间均服从负指数分布。试求: （1）此排队系统的状态转移图；（2）稳态下的概率转移平衡方程组； 3）店内有2个顾客的概率； 4）该系统的其它数量指标。 (2) 由转移图可得稳态下的差分方程组如下： / / FCFS ］排队模型，该系统的状态转移图如下: 1 P p 。 2^ ( 1 )P P 2P 3 ( 2 )E P n 1 2P n 1 (2 )P n 2 3 n P R P 2 P 0 P 3 2 P P n P n 1 1 1 2 1 2 1 2 P o （3）已知 30（人/小时） 1 1 1^— =40(人/小时)2= 丁 = 60(人/小时) 1.5 1 60 60 n P 0[1 百]1 n 1 1 2 1 F 0 1 30 3 30 40 2 60 p [1 亡1 0.4 P n

3 1 0.4 0.15 4 2 （4）系统中的平均顾客数（队长期望值）系统中顾客等待时间 9.2某商店每天开10个小时，一天平均有 90个顾客到达商店，商店的服务平均速度是每小时服务10 个，若假定顾客到达的规律是服从 Poisson 分布，商店服务时间服从负指数分布, 试求：（1）在商店前等待服务的顾客平均数。（2）在队长中多于2个人的概率。（3）在商店中平均有顾客的人数。（4）若希望商店平均顾客只有 2人，平均服务速度应提高到多少。【解】此题是属于[M/M/1]:[ / /FCFS]系统，其中： =9 （个/小时） =10（个/小时） / =9/10 (1) L q 2 /(1 )8.1 (个) (2) P(N 2) 3 0.729 ⑶ L /(1 )9 (个) ⑷L /( )2 2 9 18 13.5（个/小时） 2 2 9.3为开办一个小型理发店，目前只招聘了一个服务员，需要决定等待理发的顾客的位子应设立多少。假设需要理发的顾客到来的规律服从泊松流，平均每4分钟来一个，而理发的时间服从指数分布，平均每3分钟1人。如果要求理发的顾客因没有等待的位子而转向其他理发店的人数占要理发的人数比例为 7%时，应该安放几个位子供顾客等待？【解】此题属于[M /M /1]:[N/ / FCFS ]模型，依题意知： nP n n 0 1 P 0 1 P 0(1 2 … ) 1 （1 0.5）2 在队列中等待的平均顾客数（队列长期望值） 1P0 (1 L q 1.2 系统中顾客逗留时间 2 )2 0.4 1.2(人 ) (n 1)P n 1 1巳（ 1 -0.4 4 ____ 1 1 2 nP n 1 P n 1 ...)L 1 P o 1 ~~2 0.4(人) 1.2 30 0.04(小时) 则 P 2 1 2P 0 0.4 30 0.013（小、时）

熊伟编《运筹学》习题五详细解答

习题五 5.2用元素差额法直接给出表5-53及表5-54下列两个运输问题的近似最优解. 表 5-53 【解】表。 Objective Vallue = 824 (Minimization) 表5-54 Z=495

Objective Value = 495 (Minimization) ^Eritering: Source 1 to Deslinator A Leading: Source 3 to Desti 5.3求表5-55及表5-56所示运输问题的最优方案. (1)用闭回路法求检验数(表5-55) （2）用位势法求检验数（表5-56）【解】（1）

5.4求下列运输问题的最优解 (1) C i目标函数求最小值；(2) C2目标函数求最大值 3 5 9 2 50 7 10 15 20 60 C1 6 4 8 5 25 C 14 13 9 6 30 11 13 12 7 30 5 8 7 10 90 15 45 20 40 60 30 50 40 ⑶目标函数最小值，B i的需求为30W b i w 50, B2的需求为40, B3的需求为20< b3W 60,A i不

可达A A , B4的需求为30. 4 9 7 70 6 5 3 2 20 8 4 9 10 50 (3)先化为平衡表

5.5 (1)建立数学模型设X j (|=l,2,3;j=1,2)为甲、乙、丙三种型号的客车每天发往 B i , B 2 两城市的台班数，则 maxZ 40(80x 11 65x i 2 60夠 50冷2 50x 31 40x 32) 40x 11 40x 21 40x 31 400 40x 12 40x 22 40x 32 600 X 11 X 12 5 X 11 X 22 10 X 31 X 32 15 X j 0(i 1,2,3; j 1,2) ( 2) 写平衡运价表 132333为了平衡表简单，故表中运价没有乘以，最优解不变 (3 )最优调度方案:

熊伟编《运筹学》习题十一详细解答

习题十 11.1某地方书店希望订购最新出版的图书?根据以往经验，新书的销售量可能为 50, 100, 150或200本.假定每本新书的订购价为 4元，销售价为6元，剩书的处理价为每本 2 元.要求：（1 ）建立损益矩阵；（2）分别用悲观法、乐观法及等可能法决策该书店应订购的新书数字；（3）建立后悔矩阵，并用后悔值法决定书店应订购的新书数. （4）书店据以往统计资料新书销售量的规律见表 11 - 13,分别用期望值法和后悔值法决定订购数量；（5）如某市场调查部门能帮助书店调查销售量的确切数字，该书店愿意付出多大的调查费用。表 11- 13 表 - （2） 1 4 23（3）后悔矩阵如表11.1-2所示。表 2 3 （4）按期望值法和后悔值法决策，书店订购新书的数量都是 100本。（5）如书店能知道确切销售数字，则可能获取的利润为 X j p （x ），书店没有调查费用时 i 的利润为：50X0.2+100 >0.4+150 X0.3+200 X ）.仁115元，则书店愿意付出的最大的调查费用为 X i P （X j ） 115 i 11.2某非确定型决策冋题的决策矩阵如表 11 — 14所示: 表 11- 14

(1)若乐观系数a =0.4，矩阵中的数字是利润，请用非确定型决策的各种决策准则分别确定出相应的最优方案. (2)若表11 - 14中的数字为成本，问对应于上述决策准则所选择的方案有何变化？【解】(1)悲观主义准则：S3 ；乐观主义准则：S3 ; Lapalace准则：S3 ; Savage准则：3 ；折衷主义准则：S3。 (2 )悲观主义准则：S2 ；乐观主义准则：S3 ; Lapalace准则：S1 ; Savage准则： S1 ;折衷主义准则：S1或S2。 11.3在一台机器上加工制造一批零件共 10 000个，如加工完后逐个进行修整，则全部可以合格，但需修整费 300元.如不进行修理数据以往资料统计，次品率情况见表11- 15. (1 )用期望值决定这批零件要不要整修； (2)为了获得这批零件中次品率的正确资料，在刚加工完的一批10000件中随机抽取130 个样品，发现其中有9件次品，试修正先验概率，并重新按期望值决定这批零件要不要整修. 【解】(1)先列出损益矩阵见表 11-19 (2)修正先验概率见表11-20 表

熊伟编《运筹学》习题十一详细解答

习题十一 11.1 某地方书店希望订购最新出版的图书．根据以往经验，新书的销售量可能为50，100，150或200本．假定每本新书的订购价为4元，销售价为6元，剩书的处理价为每本2元．要求：（1）建立损益矩阵；（2）分别用悲观法、乐观法及等可能法决策该书店应订购的新书数字；（3）建立后悔矩阵，并用后悔值法决定书店应订购的新书数．（4）书店据以往统计资料新书销售量的规律见表11－13，分别用期望值法和后悔值法决定订购数量；（5）如某市场调查部门能帮助书店调查销售量的确切数字，该书店愿意付出多大的调查费用。表11－13 需求数 50 100 150 200 比例（%） 20 40 30 10 【解】（1）损益矩阵如表11.1－1所示。表11.1－1 销售订购 E 1 E 2 E 3 E 4 50 100 150 200 S 1 50 100 100 100 100 S 2 100 0 200 200 200 S 3 150 -100 100 300 300 S 4 200 -200 200 400 （2）悲观法：S 1 乐观法：S 4 等可能法：S 2或S 3。（3）后悔矩阵如表11.1－2所示。表11.1－2 E 1 E 2 E 3 E 4 最大后悔值 S 1 0 100 200 300 300 S 2 100 0 100 200 200 S 3 200 100 0 100 200 S 4 300 200 100 300 按后悔值法决策为：S 2或S 3 （4）按期望值法和后悔值法决策，书店订购新书的数量都是100本。（5）如书店能知道确切销售数字，则可能获取的利润为 ()i i i x p x ∑，书店没有调查费用时的利润为：50×0.2+100×0.4+150×0.3+200×0.1=115元，则书店愿意付出的最大的调查费用为 ()115i i i x p x -∑ 11.2某非确定型决策问题的决策矩阵如表11－14所示：表11－14 E 1 E 2 E 3 E 4 S 1 4 16 8 1 事件方案

熊伟编《运筹学》习题二详细解答

习题二 1．某人根据医嘱，每天需补充A 、B 、C 三种营养，A 不少于80单位，B 不少于150单位，C 不少于180单位．此人准备每天从六种食物中摄取这三种营养成分．已知六种食物每百克的营养成分含量及食物价格如表2-22所示．（1）试建立此人在满足健康需要的基础上花费最少的数学模型；（2）假定有一个厂商计划生产一中药丸，售给此人服用，药丸中包含有A ，B ，C 三种营养成分．试为厂商制定一个药丸的合理价格，既使此人愿意购买，又使厂商能获得最大利益，建立数学模型．表2-22 含量食物营养成分一二三四五六需要量 A 13 25 14 40 8 11 ≥80 B 24 9 30 25 12 15 ≥150 C 18 7 21 34 10 0 ≥180 食物单价（元/100g ） 0.5 0.4 0.8 0.9 0.3 0.2 【解】（1）设x j 为每天第j 种食物的用量，数学模型为 ?????? ?≥≥++++≥+++++≥++++++++++=0 1801034217181501512253092480118401425132.03.09.08.04.05.0min 65432154321654321654321654321x x x x x x x x x x x x x x x x x x x x x x x x x x x x x Z 、、、、、（2）设y i 为第i 种单位营养的价格，则数学模型为 1231231231231231 23 12123max 801501801324180.525970.4 1430210.84025340.9812100.3 11150.5,,0 w y y y y y y y y y y y y y y y y y y y y y y y =++++≤??++≤? ?++≤? ++≤??++≤??++≤? ≥? 2．写出下列线性规划的对偶问题（1）?????≥≤+-≤+-+-=0,451342max 21212121x x x x x x x x 【解】12 121212 min 42354,0w y y y y y y y y =-+-+≥-?? +≥??≥?

运筹学第3版熊伟编著习题答案

运筹学（第3版）习题答案第1章线性规划 P36 第2章线性规划的对偶理论 P74 第3章整数规划 P88 第4章目标规划 P105 第5章运输与指派问题P142 第6章网络模型 P173 第7章网络计划 P195 第8章动态规划 P218 第9章排队论 P248 第10章存储论P277 第11章决策论P304 第12章多属性决策品P343 第13章博弈论P371 全书420页第1章线性规划 1.1工厂每月生产A 、B 、C 三种产品 ,单件产品的原材料消耗量、设备台时的消耗量、资源限量及单件产品利润如表1－23所示． 310和130.试建立该问题的数学模型,使每月利润最大．【解】设x 1、x 2、x 3分别为产品A 、B 、C 的产量，则数学模型为 1231231 23123123max 1014121.5 1.2425003 1.6 1.21400 150250260310120130,,0 Z x x x x x x x x x x x x x x x =++++≤??++≤??≤≤?? ≤≤??≤≤?≥?? 1.2建筑公司需要用5m 长的塑钢材料制作A 、B 两种型号的窗架．两种窗架所需材料规格及数量如表1－24所示：

问怎样下料使得（1）用料最少；（2）余料最少．【解设x j （j =1,2,…，10）为第j 种方案使用原材料的根数，则（1）用料最少数学模型为 10 1 12342567368947910 min 2800212002600223900 0,1,2,,10 j j j Z x x x x x x x x x x x x x x x x x x j ==?+++≥? +++≥?? +++≥??+++≥??≥=?∑L （2）余料最少数学模型为 2345681012342567368947910 min 0.50.50.52800 212002********* 0,1,2,,10 j Z x x x x x x x x x x x x x x x x x x x x x x x x j =++++++?+++≥? +++≥?? +++≥??+++≥??≥=?L 1.3某企业需要制定1～6月份产品A 的生产与销售计划。已知产品A 每月底交货，市场需求没有限制，由于仓库容量有限，仓库最多库存产品A1000件，1月初仓库库存200件。1～6月份产品A 的单件成本与售价如表1－25所示。（2）当1月初库存量为零并且要求6月底需要库存200件时，模型如何变化。【解】设x j 、y j （j ＝1，2，…，6）分别为1～6月份的生产量和销售量，则数学模型为

熊伟运筹学课后习题答案1-4章

目录教材习题答案 ................................................. 错误!未定义书签。习题一 ................................................... 错误!未定义书签。习题二 ................................................... 错误!未定义书签。习题三 ................................................... 错误!未定义书签。习题四 ................................................... 错误!未定义书签。习题五 ................................................... 错误!未定义书签。习题六 ................................................... 错误!未定义书签。习题七 ................................................... 错误!未定义书签。习题八 ................................................... 错误!未定义书签。部分有图形的答案附在各章PPT文档的后面，请留意。习题一讨论下列问题：（1）在例中，假定企业一周内工作5天，每天8小时，企业设备A有5台，利用率为,设备B有7台，利用率为,其它条件不变，数学模型怎样变化．（2）在例中，如果设x j(j=1，2，…，7)为工作了5天后星期一到星期日开始休息的营业员，该模型如何变化．（3）在例中，能否将约束条件改为等式；如果要求余料最少，数学模型如何变化；简述板材下料的思路．（4）在例中，若允许含有少量杂质，但杂质含量不超过1％，模型如何变化．（5）在例中，假定同种设备的加工时间均匀分配到各台设备上，要求一种设备每台每天的加工时间不超过另一种设备任一台加工时间1小时，模型如何变化．工厂每月生产A、B、C三种产品 ,单件产品的原材料消耗量、设备台时的消耗量、资源限量及单件产品利润如表1－22所示．表1－22

熊伟运筹学(第2版)1-3章参考答案

运筹学(第2版)习题答案1--3 习题一 1.1讨论下列问题： (1)在例1.2中，如果设X j(j=l , 2,…，7)为工作了5天后星期一到星期日开始休息的营业员，该模型如何变化. (2)在例1.3中，能否将约束条件改为等式；如果要求余料最少，数学模型如何变化；简述板材下料的思路. (3)在例1.4中，若允许含有少量杂质，但杂质含量不超过1%,模型如何变化. (4)在例1.6中，假定同种设备的加工时间均匀分配到各台设备上，要求一种设备每台每天的加工时间不超过另一种设备任一台加工时间1小时，模型如何变化. ⑸在单纯形法中，为什么说当k o并且a ik 0(i 1,2,L ,m)时线性规划具有无界解。 1.2工厂每月生产A、B、C三种产品，单件产品的原材料消耗量、设备台时的消耗量、资源限量及单件产品利润如表 1 - 23所示. 表1-23 根据市场需求，预测三种产品最低月需求量分别是150、260和120，最高月需求是250、310 和130 ?试建立该问题的数学模型，使每月利润最大. 【解】设X1、X2、X3分别为产品A、B、C的产量，则数学模型为 maxZ 1 0 x-! 14x212x3 1.5x 11.2 X2 4x3 2500 3x1 1.6x 2 1.2X3 1400 150 % 250 260 X2 310 120 X3 130 为，,x3 0 1.3建筑公司需要用6m长的塑钢材料制作A、B两种型号的窗架?两种窗架所需材料规格及数量如表1 —24所示：问怎样下料使得(1)用料最少；(2)余料最少. 【解】第一步：求下料方案，见下表。

第二步：建立线性规划数学模型设X j (j=1,2, ??,? 14)为第j 种方案使用原材料的根数，则 (1)用料最少数学模型为 1 4 min Z j X j 1 2为 X 2 X 3 X 4 300 X 2 3X 5 2X 6 2X 7 X 8 % X 10 450 X 3 X 2x 8 X 3X 11 2X I 2 为 3 400 X 2 X 3 2X 4 X 7 X 9 3X 10 2X 12 3X 13 4为4 600 X j 0,j 1,2 ,L ,14 用单纯形法求解得到两个基本最优解 X ⑴=(50 ,200 ,0 ,0,84 ,0,0 ,0 ,0 ,0 ,0 ,200 ,0 ,0 );Z=534 X ⑵=(0 ,200 ,100 ,0,84 ,0,0 ,0 ,0 ,0 ,0 ,150 ,0 ,0 );Z=534 (2)余料最少数学模型为 minZ 0.6X 1 0.3X 3 0.7X 4 L 0.4X 13 0.8X i4 2X 1 X 2 X 3 X 4 300 X 2 3X 5 2X 6 2X 7 X X 9 X i0 450 X 3 X 6 2X 8 X 3X ii 2X 12 X 1 3 400 X 2 X 3 2X 4 X 7 X 9 3X i0 2X 12 3X 13 4X 14 600 X j 0, j 1,2,L ,14 用单纯形法求解得到两个基本最优解 X ⑴=(0 ,300 ,0 ,0,50 ,0,0 ,0 ,0 ,0 ,0 ,200 ,0 ,0 );Z=0，用料 550 根 X (2)=( 0 ,450 ,0 ,0,0 ,0,0 ,0 ,0 ,0 ,0 ,200 ,0 ,0 );Z=0，用料 650 根显然用料最少的方案最优。 1.4某企业需要制定1?6月份产品A 的生产与销售计划。已知产品 A 每月底交货，市场需求没有限制，由于仓库容量有限，仓库最多库存产品 A1000件，1月初仓库库存200件。1 6月份产品A 的单件成本与售价如表 1-25所示。 (1) 1?月份产品各生产与销售多少总利润最大，建立数学模型； (2) 当1月初库存量为零并且要求 6月底需要库存200件时，模型如何变化。【解】设X j 、y j (j = 1, 2,…，6)分别为1?6月份的生产量和销售量，则数学模型为

熊伟编《运筹学》习题四详细解答

习题四 4.1工厂生产甲、乙两种产品，由A、E二组人员来生产。A组人员熟练工人比较多，工作效率高，成本也高；E组人员新手较多工作效率比较低，成本也较低。例如，A组只生产甲产品时每小时生产10件，成本是50元有关资料如表4.21所示。表 4.21 二组人员每天正常工作时间都是8小时，每周5天。一周内每组最多可以加班10小时，加班生产的产品每件增加成本5元。工厂根据市场需求、利润及生产能力确定了下列目标顺序： P1：每周供应市场甲产品400件，乙产品300件 P2：每周利润指标不低于500元 P3：两组都尽可能少加班，如必须加班由A组优先加班建立此生产计划的数学模型。 4.1【解】解法一：设X1, X2分别为A组一周内正常时间生产产品甲、乙的产量，X3, X4分别为A组一周内加班时间生产产品甲、乙的产量；X5, X6分别为B组一周内正常时间生产产品甲、乙的产量，X7, X8分别为B组一周内加班时间生产产品甲、乙的产量。总利润为 80(X1 X3 X5 X7) (5055X3 45X5 50X7) 75(X2 X X6 X s) (45X2 50X4 40X6 45x0 30X1 30X2 25X3 25X4 35X5 35X6 30X7 30X8 生产时间为 A 组：0.1捲0.125X20.1X30.125X4 B 组：0.125x50.2X60.125X70.2沧数学模型为： min Z p1(d1d2) P2d3 P3(d 4 d5) P4(d6 2d?) X1 X3 X5 X7 d1 d1 400 X2 X4 X6 X8 d2 d2 300 30为30X225X325X435X535X630X730XS d3500 40 0.1X10.125X2 d4d 4 40 0.125X5 0.2X6 d5d 5 0.1X3 0.125x4 d6d6 10 0.125X70.2X8 d7d7 10 X j 0,d i ,d i 0,i 1,2丄，7; j 1,2,L ,8 解法二：设X1, X2分别为A组一周内生产产品甲、乙的正常时间，X3, X4分别为A组一周内生产产品甲、乙的加班时间；X5, X6分别为B组一周内生产产品甲、乙的正常时间，X7, X8分别为B组一周内生产产品甲、乙的加班时间。数学模型请同学们建立。

熊伟编《运筹学》习题四详细解答

习题四 4.1 工厂生产甲、乙两种产品，由Ａ、Ｂ二组人员来生产。Ａ组人员熟练工人比较多，工作效率高，成本也高；Ｂ组人员新手较多工作效率比较低，成本也较低。例如，A 组只生产甲产品时每小时生产10件，成本是50元有关资料如表4.21所示。表4.21 产品甲产品乙效率(件/小时) 成本(元/件) 效率(件/小时) 成本(元/件) A 组 10 50 8 45 B 组 8 45 5 40 产品售价(元/件) 80 75 二组人员每天正常工作时间都是8小时，每周5天。一周内每组最多可以加班10小时，加班生产的产品每件增加成本5元。工厂根据市场需求、利润及生产能力确定了下列目标顺序： P 1：每周供应市场甲产品400件，乙产品300件 P 2：每周利润指标不低于500元 P 3：两组都尽可能少加班，如必须加班由Ａ组优先加班建立此生产计划的数学模型。 4.1【解】解法一：设x 1, x 2分别为A 组一周内正常时间生产产品甲、乙的产量，x 3, x 4分别为A 组一周内加班时间生产产品甲、乙的产量；x 5, x 6分别为B 组一周内正常时间生产产品甲、乙的产量，x 7, x 8分别为B 组一周内加班时间生产产品甲、乙的产量。总利润为 135713572468246812345678 80()(50554550)75()(45504045)3030252535353030x x x x x x x x x x x x x x x x x x x x x x x x +++-+++++++-+++=+++++++ 生产时间为 A 组：12340.10.1250.10.125x x x x +++ B 组：56780.1250.20.1250.2x x x x +++ 数学模型为： 112233454671357112468221 234567833124456553min ()()(2) 400300 3030252535353030500 0.10.12540 0.1250.2400.10.Z p d d p d p d d p d d x x x x d d x x x x d d x x x x x x x x d d x x d d x x d d x ---++++ +-+-+ =++++++++++-=++++-=++++++++-=++-=++-=+－－－－－466 787712510 0.1250.2100,,0,1,2,,7;1,2,,8j i i x d d x x d d x d d i j -+-+-+??????????+-=? ?++-=?≥≥==?? L L 解法二：设x 1, x 2分别为A 组一周内生产产品甲、乙的正常时间，x 3, x 4分别为A 组一周内生产产品甲、乙的加班时间；x 5, x 6分别为B 组一周内生产产品甲、乙的正常时间，x 7, x 8分别为B 组一周内生产产品甲、乙的加班时间。数学模型请同学们建立。

运筹学第3版熊伟编著习题答案

运筹学（第3版）习题答案第1章线性规划 P36 第2章线性规划的对偶理论 P74 第3章整数规划 P88 第4章目标规划 P105 第5章运输与指派问题P142 第6章网络模型 P173 第7章网络计划 P195 第8章动态规划 P218 第9章排队论 P248 第10章存储论P277 第11章决策论P304 第12章多属性决策品P343 第13章博弈论P371 全书420页第1章线性规划 1.1 工厂每月生产A 、B 、C 三种产品 ,单件产品的原材料消耗量、设备台时的消耗量、资源限量及单件产品利润如表1－23所示． 310和130.试建立该问题的数学模型,使每月利润最大．【解】设x 1、x 2、x 3分别为产品A 、B 、C 的产量，则数学模型为 1231231 23123123max 1014121.5 1.2425003 1.6 1.21400 150250260310120130,,0 Z x x x x x x x x x x x x x x x =++++≤??++≤??≤≤?? ≤≤??≤≤?≥?? 1.2 建筑公司需要用5m 长的塑钢材料制作A 、B 两种型号的窗架．两种窗架所需材料规格及数量如表1－24所示：

熊伟编《运筹学》习题二详细解答

习题二 1 ?某人根据医嘱，每天需补充A、B、C三种营养，A不少于80单位，B不少于150 单位，C不少于180单位.此人准备每天从六种食物中摄取这三种营养成分. 已知六种食物每百克的营养成分含量及食物价格如表2-22所示.（1）试建立此人在满足健康需要的基础上花费最少的数学模型；（2）假定有一个厂商计划生产一中药丸，售给此人服用，药丸中包含有A , B , C三种营养成分?试为厂商制定一个药丸的合理价格，既使此人愿意购买，又使厂商能获得最大利益，建立数学模型. 表 2-22 1 X j j min Z 0.5% 0.4X0.8X30 .9x40.3X50.2X6 13x125x214X3 40X48X5 11X6 80 24x19x230X325X412X5 15X6 150 18x17x221X3 34X410X5 180 x1> x2、 X、X4、 X、 X6 0 (2 )设V i为第i种单位营养的价格，则数学模型为max w 80y1 150 y 2180 y3 13V1 24 y2 18y3 0.5 25y1 9y 2 7y3 0.4 14y1 30 y 221y3 0.8 40y1 25y2 34 y3 0.9 8y1 12y2 10y3 0.3 11y1 15y2 0.5 力，丫2”30 2 ?写出下列线性规划的对偶问题 max 2X14X2min w % 4y2 八X1 3X2 1 ”y1 y2 2 （1） X15X2 4 3y1 5y2 4 X1,X2 0 y1, y2 0

min w 9% 6y 2 2y 3+5y 4 10 y 5 3y i 6y 2 y 3 g 衣 2 对偶问题为： 2y i 2y 2 3 y i 5y 2 出 6 6y i y 2 2y 3 7 y i 无约束；y 2 0, y 3, 0, y 4 0, X 5 0 3 .考虑线性规划 mi nZ 12X 1 20X 2 X 1 4X 2 4 X 1 5X 2 2 2X 1 3X 2 7 X 1, X 2 0 (1) 说明原问题与对偶问题都有最优解； ⑵通过解对偶问题由最优表中观察出原问题的最优解; ⑶利用公式C B B^1求原问题的最优解； (4) 利用互补松弛条件求原问题的最优解. 【解】(1)原问题的对偶问题为 maxw 4% 2y 2 7y 3 y i y 2 2y 3 12 min Z 2x i X 2 3x 3 x 1 2X 2 10 (2) 1 2 X i 3X 2 X 3 8 X ,X 无约束，X 0 maxw 10y i 8y 2 y i y 2 2 【解】2y i 3y 2 1 y 2 3 叶无约束；y 2 0 maxZ X 1 2X 2 4X 3 3X 4 10X 1 X 2 X 3 4X 4 8 (3) 7X 1 6X 2 2X 3 5X 4 10 4X 1 8X 2 6X 3 X 4 6 X 1,X 2 0,X 3 0,X 4无约束 min w 8y 1 10y 2 6y 3 【解】 10 y 1 7y 2 4y 3 1 y 1 6y 2 8y 3 2 y 1 2y 2 6y 3 4 4y 1 5y 2 y 3 3 y 1 无约束；y 2 0, y 3 0 max Z 2X -I 3X 2 6X 3 7X 4 3X -I 2X 2 X 3 6X 4 9 6X -I 5X 3 X 4 X 1 2X 2 X 3 6 2X 4 5 X 1 10 X 1 0, X 2,X 3, X 4无约束 max Z 2X -I 3X 2 6X 3 7X 4 3X 1 2X 2 X 3 6X 4 9 6X -| 5X 3 X 4 6 【解】 X 1 2X 2 X 3 2X 4 2 X -I 5 X -I 10 X - 0, X , X , X 无约束

熊伟编《运筹学》习题十二详细解答

习题十二 12.1 证明本章中的定理4 12.2求出下列得益矩阵中所表示的对策中的混合策略纳什均衡． L R L 2，1 0，2 R 1，2 3，0 【解】设局中人1分别以21x x 和的概率选择L 和R 策略，局中人2分别以21y y 和的概率选择L 和R 策略，用方程组方法，则可得到： 1212122201x x x x x x +=+?? +=? 1212 12 20131y y y y y y +=+??+=? 解出：122/3,1/3x x ==， 123/4,1/4y y ==。混合策略纳什均衡为：G=(**,y x ) 其中： ()* * (2/3,1/3),3/4 ,1/4T T x y == 12.3 求解下列矩阵对策，其中赢得矩阵A 分别为 (1)5692354810????--??????， (2) 632745206????????-??， (3)75 91066 4132321452 34675 57 8 6????-????--???????? 【解】（1）有鞍点。最优解13(,)αβ，V G =5 (2) 有鞍点。最优解11(,)αβ，V G =2 (3) 有鞍点。最优解12(,)αβ及52(,)αβ，V G =5 12.4利用优超原则求解下列矩阵对策（1）A=13 9225 76302522 40-????? ? ??? ?-?? ， (2) 2 343 56 41324 2145734645 41 2 6A --????-????=--? ?-?????? 【解】（1） 9113 213-2256256252525630530530332762542-200305220A -???? ?????????? ??? ???=→→→→????????????????? ????? -???? - 由公式（12.19）～（12.23）得 11221221()()15a a a a +-+=-

熊伟编《运筹学》习题九详细解答

习题九 9.1某蛋糕店有一服务员，顾客到达服从λ=30人/小时的Poisson 分布，当店里只有一个顾客时，平均服务时间为1.5分钟，当店里有2个或2个以上顾客时，平均服务时间缩减至1分钟。两种服务时间均服从负指数分布。试求：（1）此排队系统的状态转移图；（2）稳态下的概率转移平衡方程组；（3）店内有2个顾客的概率；（4）该系统的其它数量指标。【解】（1）此系统为]//[:]1//[FCFS M M ∞∞排队模型，该系统的状态转移图如下：（2）由转移图可得稳态下的差分方程组如下： ?????? ?+=++=++=+=+-n n n P P P P P P P P P P P )()()(2121223211 12201 10λμμλλμμλλμμλμλ 01 1P P μλ =∴ 02122P P μμλ= 022133P P μμλ= 01 21P P n n n -=μμλ （3）已知小时）（人＝＝小时）（人＝＝小时）（人/6060 11 /40605.11/3021μμλ= 由 1i i P ∞ ==∑得 01 112 1 1 02[1]111n n n P P λμμλμλμ∞ -=-+=?? ????=+ ??-??? ? ∑ 令 1212303301 ,404602 λλρρμμ＝＝＝＝＝＝，有 11102 1 01201 12 3 4[1][1]0.4 1112 n n n n P p p p ρ ρλρρμμ----=+=+=--==

则 212031 0.40.1542 P P ρρ== ??= （4）系统中的平均顾客数（队长期望值） )(2.1) 5.01(1 4.043)1(1 ...) 321(2 22010 320101210 人=-??=-=+++===∑∑∞ =-∞ =ρρρρρρρP P P n nP L n n n n 在队列中等待的平均顾客数（队列长期望值） ) (4.02 114 .043 2.11...)...1()1(2 0112222011 1 1 人=-?-=--=+++++-=-=-=-∞ =∞ =∞ =∑∑∑ρρρρρρp L P L P nP P n L n n n n n n n q 系统中顾客逗留时间 1.2 0.04()30 L W λ = = =小时系统中顾客等待时间 )(013.030 4 .0小时== = λ q q L W 9.2某商店每天开10个小时，一天平均有90个顾客到达商店，商店的服务平均速度是每小时服务10个，若假定顾客到达的规律是服从Poisson 分布，商店服务时间服从负指数分布，试求：（1）在商店前等待服务的顾客平均数。（2）在队长中多于2个人的概率。（3）在商店中平均有顾客的人数。（4）若希望商店平均顾客只有2人，平均服务速度应提高到多少。【解】此题是属于]//[:]1//[FCFS M M ∞∞系统，其中： λ=9（个/小时） μ=10(个/小时) μλρ/==9/10 (1) 1.8)1/(2 =-=ρρq L （个） (2) 729.0)2(3 ==>ρN P (3) 9)1/(=-= ρρL （个） (4) /()2L λμλ=-= 2918 13.522 λλμ++= ==(个/小时) 9.3为开办一个小型理发店，目前只招聘了一个服务员，需要决定等待理发的顾客的位子应设立多少。假设需要理发的顾客到来的规律服从泊松流，平均每4分钟来一个，而理发的时间服从指数分布，平均每3分钟1人。如果要求理发的顾客因没有等待的位子而转向其他理发店的人数占要理发的人数比例为7％时，应该安放几个位子供顾客等待？【解】此题属于]//[:]1//[FCFS N M M ∞模型,依题意知：

熊伟编《运筹学》附录D判断题答案

附录D判断题答案 (把它下载到你的电脑，编辑，把字体放大就行了线性规划 1.X不一定有最优解 2.V 3.X不一定 4.V 5.V 6.X是非线性规划模型，但可以转化为线性规划模型 7.V 8.V 9.X不一定是可行基，基本可行解对应的基是可行基 10.V 11.V 12.V 13.V 14.X原问题可能具有无界解 15.V 16.V 17.V 18.V 19.X应为|B|工0 20.X存在为零的基变量时，最优解是退化的；或者存在非基变量的检验数为零时，线性规划具有多重最优解线性规划的对偶理论 21.V 22.V 23.X不一定 24.V 25.X对偶问题也可能无界 26.( 1) X 应为CX*> Y*b ( 2) V (3) V ( 4) V (5) V (6) V 27.V 28.X应为对偶问题不可行 29.X应为最优值相等 30.X不一定 31.X影子价格是单位资源对目标函数的贡献 32.X用单纯形法计算；或原问题不可行对偶问题可行时用对偶单纯形法计算 33.X原问题无可行解 34.X求解原问题 bi I c u - bi , c 35.X应为max | ir 0 b r min | ir 0 i ir ir 36.V 37.V 38.X不一定 39.V 40.X同时变化时最优解可能发生变化整数规划 41.X取整后不一定是原问题的最优解 42.X称为混和整数规划 43.V 44.V 45.V 46.V 47.V 48.V n 49.X应是a ij x j b i—My i j 1 50.V 目标规划 51.X正负偏差变量全部非负 52.V 53.V 54.X至少一个等于零 55.V 56.X应为min Z d 57.V 58.X—定有满意解 59.V 60.V 运输与指派问题 61.X 唯一 62.X变量应为6个 63.X—定有最优解 64.V 65.V 66.有可能变量组中其它变量构成闭回路 67.V 68.X有mn个约束

运筹学答案(熊伟)下

熊伟编《运筹学》习题十详细解答

运筹学

熊伟编《运筹学》习题九详细解答

熊伟编《运筹学》习题五详细解答

熊伟编《运筹学》习题十一详细解答

熊伟编《运筹学》习题十一详细解答

熊伟编《运筹学》习题二详细解答

运筹学第3版熊伟编著习题答案

熊伟运筹学课后习题答案1-4章

熊伟运筹学(第2版)1-3章参考答案

熊伟编《运筹学》习题四详细解答

熊伟编《运筹学》习题四详细解答

运筹学第3版熊伟编著习题答案

熊伟编《运筹学》习题二详细解答

熊伟编《运筹学》习题十二详细解答

熊伟编《运筹学》习题九详细解答

熊伟编《运筹学》附录D判断题答案

相关文档

最新文档