文科《概率与统计》高考常考题型专题训练

文科《概率与统计》高考常考题型专题训练

1．流行性感冒（简称流感）是流感病毒引起的急性呼吸道感染，是一种传染性强、传播速度快的疾病．其

主要通过空气中的飞沫、人与人之间的接触或与被污染物品的接触传播．流感每年在世界各地均有传播，在我国北方通常呈冬春季流行，南方有冬春季和夏季两个流行高峰．儿童相对免疫力低，在幼儿园、学校等人员密集的地方更容易被传染．某幼儿园将去年春期该园患流感小朋友按照年龄与人数统计，得到如下数据：

（1）求y 关于x 的线性回归方程；

（2）计算变量x 、y 的相关系数r （计算结果精确到0.01），并回答是否可以认为该幼儿园去年春期患流感人数与年龄负相关很强？（若[]0.75,1r ∈，则x 、y 相关性很强；若[

)0.3,0.75r ∈，则x 、

y 相关性一般；若[]0,0.25r ∈，则x 、y 相关性较弱．）

57.47≈．

参考公式：()()()

1

1

2

2

21

1

?n n

i

i

i i

i i n

n

i

i

i i x x y y x y nxy

b

x x x

nx

====---==

--∑∑∑∑，

相关系数()()

n

i

i

x x y y r --=

∑．

1．【解析】（1）由题意得，2345645x ++++=

=，2222171410

175

y ++++==，

()()()

()()()()

()()5

1

5

2

2

2

2

2

2

1

2515001327? 3.221012

i

i

i i

i x x y y b x x ==---?+-?+?+?-+?-===--+-+++-∑∑，

?17 3.2429.8a y bx

=-=+?=， 故y 关于x 的线性回归方程为 3.229.8y x =-+；

（2）

()() ()

()

1

22

11

0.97

10108330

n

i i

i

n n

i i

i i

x x y y

r

x x y y

=

==

--

===≈-

?

-?-

∑

∑∑

，

r

∴<，说明x、y负相关，又[]

0.75,1

r∈，说明x、y相关性很强．

因此，可以认为该幼儿园去年春期患流感人数与年龄负相关很强．

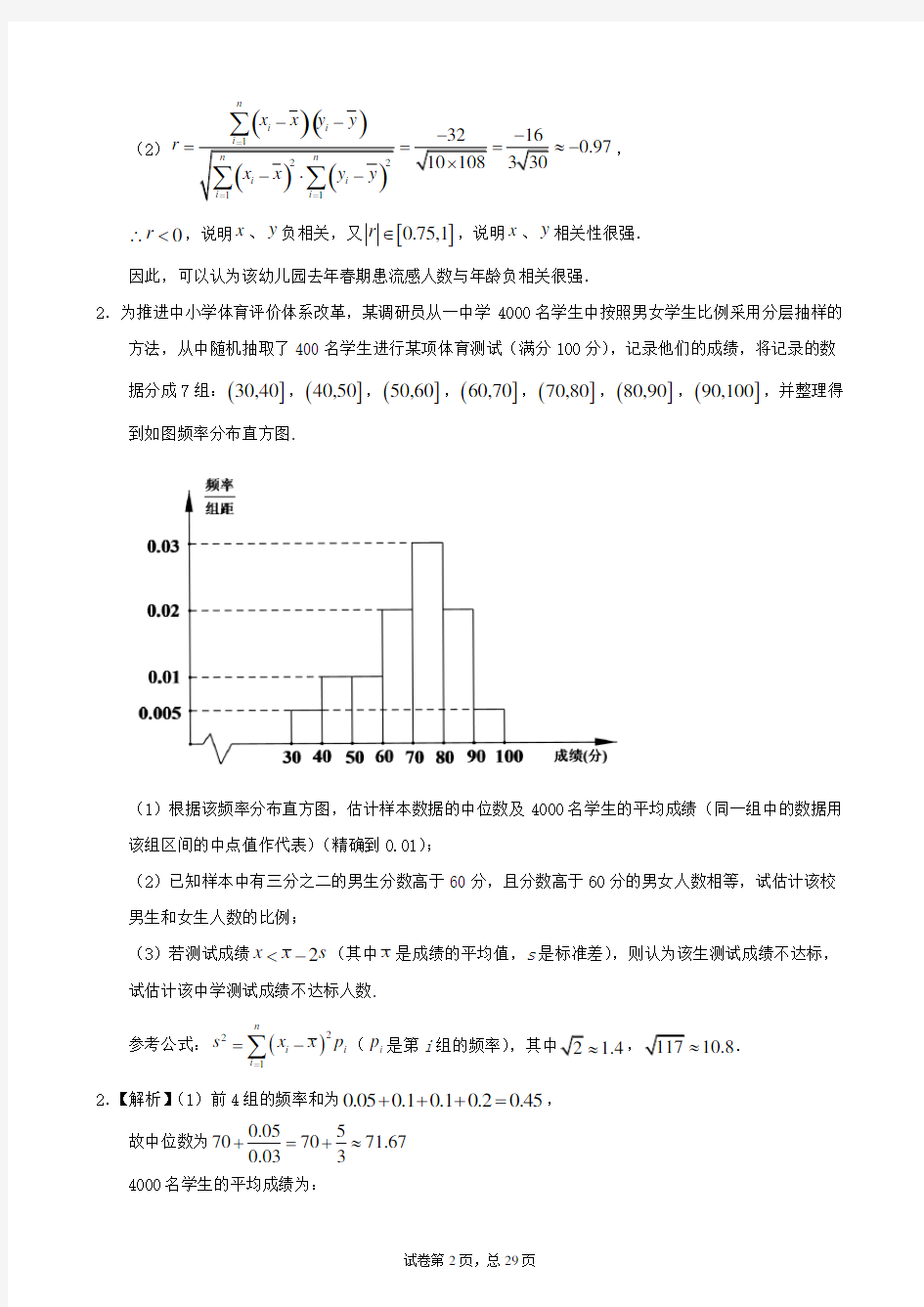
2．为推进中小学体育评价体系改革，某调研员从一中学4000名学生中按照男女学生比例采用分层抽样的方法，从中随机抽取了400名学生进行某项体育测试（满分100分），记录他们的成绩，将记录的数据分成7组：(]

30,40，(]

40,50，(]

50,60，(]

60,70，(]

70,80，(]

80,90，(]

90,100，并整理得到如图频率分布直方图.

（1）根据该频率分布直方图，估计样本数据的中位数及4000名学生的平均成绩（同一组中的数据用该组区间的中点值作代表）（精确到0.01）；

（2）已知样本中有三分之二的男生分数高于60分，且分数高于60分的男女人数相等，试估计该校男生和女生人数的比例；

（3）若测试成绩2

x x s

<-（其中x是成绩的平均值，s是标准差），则认为该生测试成绩不达标，试估计该中学测试成绩不达标人数.

参考公式：()2

2

1

n

i i

i

s x x p

=

=-

∑（i p是第i组的频率）2 1.4

≈11710.8

≈.

2．【解析】（1）前4组的频率和为0.050.10.10.20.45

+++=，

故中位数为

0.055

707071.67

0.033

+=+≈

4000名学生的平均成绩为：

0.05350.1450.1550.2650.3750.2850.059569?+?+?+?+?+?+?=；

（2）由频率分布直方图得样本中高于60分的人数占总人数的0.75， 又因为分数高于60分的男女人数相等，

故高于60分的男生、女生人数均为4000.750.5150??=人， 又因为样本中有三分之二的男生分数高于60分， 所以样本中共有男生的2

1502253

÷

=人，女生175人， 又因为样本是按照男女学生比例采用分层抽样的方法得到， 故该校男生和女生人数的比例为225:1759:7=； （3）()

()()2

2

22

1

35690.0545690.1n

i i i s x x p ==

-=-?+-?∑()255690.1+-?

()()2

2

65690.275690.3+-?+-?()()2

2

85690.295690.05234+-?+-?=

所以234211715.12s =

=?≈，26915.12238.76x s -=-?=

故测试成绩2x x s <-占比为0.050.8760.0438?=， 该中学测试成绩不达标人数约为0.0438*******?≈.

3．为了解某中学学生对《中华人民共和国交通安全法》的了解情况，调查部门在该校进行了一次问卷调

查（共12道题），从该校学生中随机抽取40人，统计了每人答对的题数，将统计结果分成[)0,2，[)2,4，

[)4,6，[)6,8，[)8,10，[]10,12六组，得到如下频率分布直方图.

（1）若答对一题得10分，未答对不得分，估计这40人的成绩的平均分（同一组中的数据用该组区间的中点值作代表）；

（2）若从答对题数在[)2,6内的学生中随机抽取2人，求恰有1人答对题数在[)2,4内的概率. 3．【解析】（1）因为答对题数的平均数约为

()10.02530.02550.037570.12590.1875110.1?+?+?+?+?+?27.9?=.

所以这40人的成绩的平均分约为7.91079?=.

（2）答对题数在[)2,4内的学生有0.0252402??=人，记为A ，B ；

答对题数在[)4,6内的学生有0.03752403??=人，记为c ，d ，e .

从答对题数在[)2,6内的学生中随机抽取2人的情况有(),A B ，(),A c ，(),A d ，(),A e ，(),B c ，

(),B d ，(),B e ，(),c d ，(),c e ，(),d e ，共10种，

恰有1人答对题数在[)2,4内的情况有(),A c ，(),A d ，(),A e ，(),B c ，(),B d ，(),B e ，共6种， 故所求概率63

105

P =

=. 4．某商店销售某海鲜，统计了春节前后50天海鲜的需求量x ，（1020x ≤≤，单位：公斤），其频率分布

直方图如图所示，该海鲜每天进货1次，商店每销售1公斤可获利50元；若供大于求，剩余的削价处理，每处理1公斤亏损10元；若供不应求，可从其它商店调拨，销售1公斤可获利30元.假设商店每天该海鲜的进货量为14公斤，商店的日利润为y 元.

（1）求商店日利润y 关于需求量x 的函数表达式； （2）假设同组中的每个数据用该组区间的中点值代替. ①求这50天商店销售该海鲜日利润的平均数；

②估计日利润在区间[]580760，

内的概率. 4．【解析】（1）商店的日利润y 关于需求量x 的函数表达式为：

()()50143014,1420

501014,1014x x y x x x ??+?-≤≤?=?-?-≤

化简得：30280,1420

60140,1014x x y x x +≤≤?=?

-≤

（2）①由频率分布直方图得：

海鲜需求量在区间[)10,12的频率是20.080.16?=；

海鲜需求量在区间[)12,14的频率是20.120.24?=； 海鲜需求量在区间[)14,16的频率是20.150.30?=； 海鲜需求量在区间[)16,18的频率是20.100.20?=； 海鲜需求量在区间[]18,20的频率是20.050.10?=； 这5050天商店销售该海鲜日利润y 的平均数为：

()()()(116014100.16136014100.24153020140.301730?-??+?-??+?+??+?+

)()20140.20193020140.1083.2153.621915885698.8??+?+??=++++=（元）

②由于14x =时，30142806014140700?+=?-=

显然30280,142060140,1014x x y x x +≤≤?=?

-≤

在区间[]10,20上单调递增， 58060140y x ==-，得12x =； 76030280y x ==+，得16x =；

日利润y 在区间[]

580,760内的概率即求海鲜需求量x 在区间[]12,16的频率：

0.240.300.54+=

5． 2011年，国际数学协会正式宣布，将每年的3月14日设为国际数学节，来源是中国古代数学家祖冲

之的圆周率，为庆祝该节日，某校举办数学趣味知识竞赛活动，参与竞赛的文科生与理科生人数之比为1:3，且成绩分布在[]40,100，分数在[)80,90，[)90,100分别获二等奖和一等奖．按文理科用分层抽样的方法抽取200人的成绩作为样本，得到成绩的频率分布直方图．

（1）填写下面的22?列联表，能否有超过95%的把握认为“获奖与学生的文理科有关”？ 文科生 理科生 合计 获奖 5 不获奖

（2）将上述调查所得的频率视为概率，现从参赛学生中，通过分层抽样的方法从这些获奖人中随机抽取4人，再从这4人中任意选取2人，求2人均获二等奖的概率． 临界值表：

参考格式：()()()()()

2

2

n ad bc K a b c d a c b d -=++++，其中n a b c d =+++．

5．【解析】（1）补全22?列联表如下表．

()2

22005115354525

4.167 3.84150150401606

K ??-?==≈>???．

所以有超过95%的把握认为“获奖与学生的文理科有关”． （2）由已知可得，分数在[)80,90获二等奖的参赛学生中抽取3人， 分数在[]90,100获一等奖的参赛学生中抽取1人． 记二等奖的3人分别为a ，b ，c ，一等奖的1人为A ， 事件E 为“从这4人中抽取2人且这2人均是二等奖”．

从这4人中随机抽取2人的基本事件为(),a b ，(),a b ，(),a A ，(),b c ，

(),b A ，(),c A ，

，共6种，

其中2人均是二等奖的情况有(),a b ，(),a b ，(),b c 共3种， 由古典概型的概率计算公式得()31

62

P E =

=．

故2人均获二等奖的概率为

12

． 7．为增强学生法治观念，营造“学宪法、知宪法、守宪法”的良好校园氛围，某学校开展了“宪法小卫

士”活动，并组织全校学生进行法律知识竞赛.现从全校学生中随机抽取50人，统计他们的竞赛成绩，并得到如表所示的频数分布表.

（Ⅰ）求频数分布表中的m 的值，并估计这50名学生竞赛成绩的中位数（精确到0.1）；

（Ⅱ）将成绩在[]70,100内定义为“合格”，成绩在[)0,70内定义为“不合格”.请将列联表补充完整.

试问：是否有95%的把握认为“法律知识的掌握合格情况”与“是否是高一新生”有关？说明你的理由；

（Ⅲ）在（Ⅱ）的前提下，在该50人中，按“合格与否”进行分层抽样，随机抽取5人，再从这5人中随机抽取2人，求恰好2人都合格的概率. 附：

22

()()()()()

n ad bc K a b c d a c b d -=++++，n a b c d =+++.

7．【解析】（Ⅰ）50(5151512)3m =-+++=.设成绩的中位数为x ，

则

515151(70)505002x ++-?=，解得1

7373.33

x =+≈. （Ⅱ）补全2×2列联表如下所示：

22

()()()()()

n ad bc K a b c d a c b d -=++++2

50(1261418)26243020??-?=

??? 4.327 3.841≈>， 所以有95%的把握认为“法律知识的掌握合格情况”与“是否是高一新生”有关. （Ⅲ）分层抽样的比例为

515010

=，故抽取的5人中成绩合格的有1

30310?=（人），

分别记为a ，b ，c ；成绩不合格的有1

20210

?=（人），分别记为m ，n . 从5人中随机抽取2人的基本事件有

ab ，ac ，bc ，am ，an ，bm ，bn ，cm ，cn ，mn ，共10种，

2人都合格的基本事件有ab ，ac ，bc ，共3种， 所以恰好2人都合格的概率3

0.310

P =

=. 9．某种产品的质量以其质量指标值衡量，质量指标值越大表明质量越好，记其质量指标值为M ，当85

M ≥时，产品为一级品；当7585M ≤<时，产品为二级品；当7075M ≤<时，产品为三级品.现用两种新配方（分别称为A 配方和B 配方）做实验，各生产了100件这种产品，并测量了每件产品的质量指标值，得到下面试验结果：

A 配方的频数分布表

B 配方的频数分布表

（1）从A 配方生产的产品中按等级分层抽样抽取5件产品，再从这5件产品中任取3件，求恰好取到1件二级品的频率；

（2）若这种新产品的利润率y 与质量指标M 满足如下条件：2

2,85,5,7585,,7075,t M y t M t M ≥??=≤

，其中

10,7t ??

∈ ???

，请分别计算两种配方生产的产品的平均利润率，如果从长期来看，你认为投资哪种配方的产品平均利润率较大?

9．【解析】（1）由题知，按分层抽样抽取的5件产品中有2件为二级品，记为a ，b ，有3件为一级品，

记为x ，y ，z ，

从5件产品中任取3件共有10种取法，枚举如下：(,,)a b x ，(,,)a b y ，(,,)a b z ，(,,)a x y ，(,,)a x z ，

(,,)a y z ，(,,)b x y ，(,,)b x z ，(,,)b y z ，(,,)x y z

其中恰好取到1件二级品共有6种取法，所以恰好取到1件二级品的概率为

63

105

=. （2）由题知A 配方生产的产品平均利润率22(1030)5(4020)()20.6100t t

E A t t +?++==+，

B 配方生产的产品平均利润率2225(1015)5(3040)() 1.30.7100

t t t

E B t t ++?++?==+，

所以2

()()0.70.10.1(71)E A E B t t t t -=-=-， 因为1

07

t <<

，所以()()E A E B <，所以投资B 配方的产品平均利润率较大. 10．某工厂生产了一批零件，从中随机抽取100个作为样本，测出它们的长度（单位：厘米），按数据分

成[]10,15，(]15,20，(]20,25，(]25,30，(]30,355组，得到如图所示的频率分布直方图．

（1）估计该工厂生产的这批零件长度的平均值（同一组中的每个数据用该组区间的中点值代替）； （2）若用分层抽样的方式从第1组和第5组中抽取5个零件，再从这5个零件中随机抽取2个，求

抽取的零件中恰有1个是第1组的概率． 10．【解析】

（1）由频率分布直方图可得各组频率依次为0.08，0.18，0.4，0.22，0.12， 则这批零件长度的平均值为

12.50.0817.50.1822.50.427.50.2232.50.1223.1x =?+?+?+?+?=．

（2）由题意可知第1组和第5组的零件数分别是0.081008?=和0.1210012?=， 则应从第1组中抽取5

82812

?=+个零件，记为A ，B ；应从第5组中抽取3个零件，记为c ，d ，e ．

从这5个零件中随机抽取2个的情况有AB ，Ac ，Ad ，Ae ，Bc ，Bd ，Be ，cd ，ce ，de ，共10种，

其中符合条件的情况有Ac ，Ad ，Ae ，Bc ，Bd ，Be ，共6种． 故所求概率63105

P =

=． 11．搪瓷是在金属坯体表面涂搪瓷釉而得到的制品．曾经是人们不可或缺的生活必备品，厨房用具中的锅

碗瓢盆；喝茶用到的杯子，洗脸用到的脸盆；婚嫁礼品等，它浓缩了上世纪整整一个时代的记忆．某搪瓷设计公司新开发了一种新型复古搪瓷水杯，将其细分成6个等级，等级系数X 依次3，4，5，6，7，8，该公司交给生产水平不同的A 和B 两个厂生产，从B 厂生产的搪瓷水杯中随机抽取30件，相应的等级系数组成一个样本，数据如图所示．

（1）依据图表，若从上述等级系数为7和8的搪瓷水杯中抽取2件，求这两件全部来自等级系数为8的搪瓷水杯的概率；

（2）若A 厂生产搪瓷水杯的等级系数的平均值为6，在电商平台上A 厂生产的搪瓷水杯的零售价为36元/件，B 厂生产的搪瓷水杯的零售价为30元/件．设L =

产品等级系数的平均值

产品零售价

，若以L 的

值越大，产品越具可购买性为判断标准，根据以上数据，哪个工厂的产品更具可购买性？说明理由． 11．【解析】（1）设等级系数为7的搪瓷水杯为A ，B ，C ，等级系数为8的搪瓷水杯为a ，b ，c ，

则从中抽取2件的基本事件为(),A B ，(),A C ，(),A a ，(),A b ，(),A c ，(),B C ，

(),B a ，(),B b ，(),B c ，(),C a ，(),C b ，(),C c ，(),a b ，(),a c ，(),b c ，

共15种，

其中两件全部来自等级系数为8的搪瓷水杯的基本事件为(),a b ，(),a c ，(),b c ， 共3种，所以概率为

31

155

=． （2）A 厂的产品更具可购买性，理由如下：

将频率视为概率，可得B 厂生产的搪瓷水杯的等级系数的平均值为

394656637383

4.830

X ?+?+?+?+?+?=

=，

即B 厂生产的搪瓷水杯的等级系数的平均值等于4.8，

因为A 厂生产搪瓷水杯的等级系数的平均值等于6，价格为36元/件， 所以61366

A L =

=． 因为B 厂生产的搪瓷水杯的等级系数的平均值等于4.8，价格为30元/件， 所以 4.8

0.1630

B L =

=． 因为

1

0.166

>，故A 厂生产的搪瓷水杯更具可购买性． 12．为了检测某种抗病毒疫苗的免疫效果，研究人员将疫苗注射到200只小白鼠体内，一段时间后测量小

白鼠的某项指标值，按[)0,20，[)20,40，[)40,60，[)60,80，[]80,100分组，绘制频率分布直方图如图所示，并经进一步检测，发现小白鼠体内产生抗体的共有160只，其中该项指标值不小于60的小白鼠有110只.

（1）求a 值；

（2）求200只小白鼠该项指标值的平均数；

（3）填写下面的22?列联表，并根据列联表判断是否有95%的把握认为注射疫苗后小白鼠产生抗体与指标值不小于60有关？

参考公式：()

()()()()2

2n ad bc K a b c d a c b d -=++++，其中n a b c d =+++.

12．【解析】（1）由各频率之和为1，可得：

0.0025200.0062520200.025200.0075201a ?+?+?+?+?=，解得0.00875a =.

（2）200只小白鼠某项指标值的平均数

0.002520100.0062520300.0087520

x =??+??+?500.02520700.0075209061.5?+??+??=.

（3）由频率分布直方图，200只小白鼠某项指标值的数据分布为：

在[)0,20内有0.00252020010??=个；[)20,40内有0.006252020025??=个；

[)40,60内有0.008752020035??=个；[)60,80内有0.025********??=个； []80,100内有0.00752020030??=个；

由已知，小白鼠体内产生抗体的共有160只，其中指标值不小于60的有110只，故有抗体且指标值小于60的有50只；而指标值小于60的小白鼠共有10253570=＋＋只，所以指标值小于60没有抗体的小白鼠有20，同理，指标值不小于60没有抗体的小白鼠有20只，故列联表如下：

由(

)2

220010002200 4.945 3.8411604070130

K ?-=≈>??? 所以有95%的把握认为注射疫苗后小白鼠产生抗体与指标值不小于60有关.

13．党的十九大提出，要推进绿色发展，倡导简约适度、绿色低碳的生活方式.天然气作为一种清洁高效

能源，不仅可以优化能源结构，缓解供需矛盾，而且对于改善环境、提高人民生活质量和实现可持续发展都起到十分重要的作用.某研究小组为了研究燃气灶烧水如何节省燃气的问题设计了一个实验，并获得了燃气开关旋钮旋转的弧度数x 与烧开一壶水所用时间y 的一组数据，且作了一定的数据处理（如下表），得到了散点图（如图）.

x

y

ω

()

2

10

1

i

i x x =-∑

()

2

10

1

i

i ωω=-∑

()()

10

1

i

i

i x x y

y =--∑

()()10

1

i

i

i y y ωω=--∑

1.47

20.6 0.78

2.35 0.81

19.3-

16.2

表中21i i x ω=，101

110i i ωω==∑.

（1）根据散点图判断，y a bx =+与2d

y c x

=+

哪一个更适宜作烧水时间y 关于开关旋钮旋转的弧度数x 的回归方程类型？（不必说明理由）并求出y 关于x 的回归方程；

（2）若旋转的弧度数x 与单位时间内煤气输出量t 成正比，那么x 为多少时，烧开一壶水最省煤气？ 附：对于一组数据()11,u v ，()22,u v ，()33,u v ，…，(),n n u v ，其回归直线v u αβ=+的斜率和截距

的最小二乘估计分别为()()

()

1

2

1

n

i

i

i n

i

i v v u u u u β==--=

-∑∑，v u αβ=-.

13．【解析】（1）2

d

y c x =+

更适宜. 令21

x

ω

=

，则y c d ω=+. 由公式可得：()()

()

10

1

10

2

1

16.2

200.81

i

i

i i

i y y d ωωωω==--=

=

=-∑∑， 20.3200.785c y d ω=-=-?=，所以所求回归方程为2

205y x =+

. （2）设t kx =，则煤气用量2202020552520k k

S yt kx kx kx k x x x

??==+=+≥?= ??

?， 当且仅当205k

kx x

=

时取“=”，即2x =时，煤气用量最小. 14．加班，系指除法定或者国家规定的工作时间外，即正常工作日延长工作时间或者双休日以及国家法定

假期期间延长工作时间.有的工作人员在正常工作日不能积极主动工作，致使有的工作任务要到正常工作日延长工作时间完成，这不能称为“加班”，只有建立合理的考核方案，才能调动广大工作人员的积极性.某劳动组织对“工作时间”的评价标准如下表： 每天的工作时间(单位：小时) [)6,8 [)8,10 [)10,12 []12,14

评价级别

良好

普通加班 严重加班

超重加班

2019年5月1日，该劳动组织从某单位某个月中随机抽取10天“工作时间”的统计数据绘制出的频率分布直方图如下：

（1）若严重加班的天数是普通加班天数的2倍，求m ，n 的值；

（2）在（1）条件下，若从这10天中评价级别是“良好”或“普通加班”的天数里随机抽取2天，求“这2天的‘工作时间’属于同一评价级别”的概率.

14．【解析】（1）依题意

1 3221

5

1

2

10

m n n

n

m

m

?

?+?==

??

??

?

??

=

??=

??

?

.

（2）由（1）可知这10天中评价级别是“良好”有

1

2102

10

??=天，设为,a b；评价级别是“普通加班”有

1

2102

10

??=天，设为,c d.从中抽取2天，所有可能为,,,,,

ab ac ad bc bd cd共6种，其中这2天的“工作时间”属于同一评价级别的为,

ab cd共2种，所以“这2天的‘工作时间’属于同一评价级别”的概率为

21

63

=.

15．搪瓷是在金属坯体表面涂搪瓷釉而得到的制品.曾经是人们不可或缺的生活必备品，厨房用具中的锅碗瓢盆；喝茶用到的杯子；洗脸用到的脸盆；婚嫁礼品等，它浓缩了上世纪整整一个时代的记忆.某搪瓷设计公司新开发了一种新型复古搪瓷水杯，将其细分成6个等级，等级系数X依次3，4，5，6，7，8，该公司交给生产水平不同的A和B两个广生产，从B厂生产的搪瓷水杯中随机抽取30件，相应的等级系数组成一个样本，数据如图所示：

（1）依据上表，若从上述等级系数为7和8的搪瓷水杯中抽取2件，求这2件全部来自等级系数为8的搪瓷水杯的概率；

（2）下图是5位网友对两厂生产的搪瓷水杯对比评分图，根据图表，利用评分均值和标准差比较两种搪瓷水杯的评分情况，并说明理由.

15．【解析】（1）设等级系数为7的搪瓷水杯为A ，B ，C ，等级系数为8的搪瓷水杯为a ，b ，c ，

则从中抽取2件的基本事件为

(),A B ，(),A C ，(),A a ，(),A b ，(),A c ，(),B C ，(),B a ，(),B b ，(),B c ，(),C a ，(),C b ，(),C c ，(),a b ，(),a c ，(),b c ，共15种，

其中2件全部来自等级系数为8的搪瓷水杯的基本事件为(),a b ，(),a c ，(),b c ，共3种， 所以31

155

P =

=. （2）因为()467895 6.8B x =++++÷=，所以B 厂生产的搪瓷水杯的评分平均分为6.8，标准差为

()()()()()22222

14 6.86 6.87 6.88 6.89 6.8 1.725S ??=

-+-+-+-+-=?

?， 所以B 厂生产的搪瓷水杯的评分标准差为1.72，

因为()56 6.5785 6.5A x =++++÷=，所以A 厂生产的搪瓷水杯的评分平均分为6.5，

()()()()()22222

15 6.56 6.5 6.5 6.57 6.58 6.515S ??=

-+-+-+-+-=?

? 所以A 厂生产的搪瓷水杯的评分标准差为1，

综上，B 厂生产的糖瓷水杯的评分的均值较高；A 厂生产的搪瓷水杯的评分的标准差较小，比较稳定.

16．新型冠状病毒疫情发生后，口罩的需求量大增，某口罩工厂为提高生产效率，开展技术创新活动，提

出两种新的生产方式.为比较两种生产方式的效率，选取80名工人，将他们随机分成两组，每组40人，第一组工人用第一种生产方式，第二组工人用第二种生产方式. 第一种生产方式40名工人完成同一生产任务所用时间(单位：min )如表

68 72 85 77 83 82 90 83 89 84 88 87 76 91 79 90 87 91 86 92 88 87 81 76 95 94 63 87 85 71 96

63

74

85

92

99

87

82

75

69

第二种生产方式40名工人完成同一生产任务所用时间(单位：min )如饼图所示：

（1）填写第一种生产方式完成任务所用时间的频数分布表并作出频率分布直方图； 生产时间 [)60,70

[)70,80

[)80,90

[)90,100

频数

（2）试从饼图中估计第二种生产方式的平均数；

（3）根据频率分布图和饼图判断哪种生产方式的效率更高？并说明理由.

16．【解析】（1）根据第一种生产方式40名工人完成同一生产任务所用时间的表格数据，可得：

生产时间 [)60,70

[)70,80

[)80,90

[)90,100

频数

4

8

18

10

则所用时间的频数分布表并作出频率分布直方图：

（2）根据平均数的计算公式，试从饼图中估计第二种生产方式的平均数为：

?+?+?+?=

650.25750.5850.2950.0575.5min

（3）从频率分布直方图中估计第一种生产方式的平均数为：

?+?+?+?=

650.1750.2850.45950.2583.5min

从平均数的角度发现：

用第一种生产方式的工人完成生产任务平均所需时间高于80分钟；

用第二种生产方式的工人完成生产任务平均所需时间低于80分钟.

因此第二种生产方式的效率更高.

18．某校为缓解高三学生的高考压力，经常举行一些心理素质综合能力训练活动，经过一段时间的训练后从该年级800名学生中随机抽取100名学生进行测试，并将其成绩分为A、B、C、D、E五个等级，统计数据如图所示（视频率为概率），根据图中抽样调查数据，回答下列问题：

（1）试估算该校高三年级学生获得成绩为B的人数；

（2）若等级A、B、C、D、E分别对应100分、90分、80分、70分、60分，学校要求当学生获得的等级成绩的平均分大于90分时，高三学生的考前心理稳定，整体过关，请问该校高三年级目前学生的考前心理稳定情况是否整体过关？

（3）以每个学生的心理都培养成为健康状态为目标，学校决定对成绩等级为E的16名学生（其中男生4人，女生12人）进行特殊的一对一帮扶培训，从按分层抽样抽取的4人中任意抽取2名，求恰好抽到1名男生的概率.

18．【解析】（1）从条形图中可知这100人中，有56名学生成绩等级为B，

故可以估计该校学生获得成绩等级为B 的概率为

5614

10025

=， 则该校高三年级学生获得成绩等级为B 的人数约有14

80044825

?=. （2）这100名学生成绩的平均分为()1

321005690780370260100

?+?+?+?+? 91.3=（分）

， 因为91.390>，所以该校高三年级目前学生的“考前心理稳定整体”已过关.

（3）按分层抽样抽取的4人中有1名男生，3名女生，记男生为a ，3名女生分别为1b ，2b ，3b .从中抽取2人的所有情况为1ab ，2ab ，3ab ，12b b ，13b b ，23b b ，共6种情况，其中恰好抽到1名男生的有1ab ，2ab ，3ab ，共3种情况，故所求概率12

P =

. 19．2019年6月25日，《固体废物污染环境防治法(修订草案)》初次提请全国人大常委会审议，草案对“生

活垃圾污染环境的防治”进行了专项规定.某小区采取一系列措施，宣传垃圾分类的知识与意义，并采购分类垃圾箱.为了了解垃圾分类的效果，该小区物业随机抽取了200位居民进行问卷调查，每位居民对小区采取的措施给出“满意”或“不满意”的评价.根据调查结果统计并做出年龄分布条形图和持不满意态度的居民的结构比例图，如图，在这200份问卷中，持满意态度的频率是0.65.

（1）完成下面的22?列联表，并判断能否有95﹪的把握认为“51岁及以上”和“50岁及以下”的居民对该小区采取的措施的评价有差异

满意 不满意 总计 51岁及以上的居民 50岁及以下的居民 总计

200

（2）按“51岁及以上”和“50岁及以下”的年龄段采取分层抽样的方法从中随机抽取5份，再从这5份调查问卷中随机抽取2份进行电话家访，求电话家访的两位居民恰好一位年龄在51岁及以上，另一位年龄在50岁及以下的概率.

20()P K k ≥

0.050 0.025 0.010 0.005 0.001