水力学模拟题及答案

水力学(二)模拟试题
-判断题:(20分)
1. 液体边界层的厚度总是沿所绕物体的长度减少的。()
2. 只要是平面液流即二元流,流函数都存在。()
3. 在落水的过程中,同一水位情况下,非恒定流的水面坡度比恒定流时小,因而其流量
亦小。()
4. 渗流模型中、过水断面上各点渗流流速的大小都一样,任一点的渗流流速将与断面平
均流速相等。()
5. 正坡明槽的浸润线只有两种形式,且存在于a、c两区。()
6. 平面势流的流函数与流速势函数一样是一个非调和函数。()
7. 边界层内的液流型态只能是紊流。()
8. 平面势流流网就是流线和等势线正交构成的网状图形。()
9. 达西公式与杜比公式都表明:在过水断面上各点的惨流流速都与断面平均流速相等。
()
10. 在非恒定流情况下,过水断面上的水面坡度、流速、流量水位的最大值并不在同一时
刻出现。()
二
填空题:(20分)
1. 流场中,各运动要素的分析方法常在流场中任取一个微小平行六面体来研究,那么微
小平行六面体最普遍的运动形式有: , ,四种。
2. 土的渗透恃性由:,二方面决疋。
3. 水击类型有:,两类。
4.泄水建筑物下游衔接与消能措施主要有? ?
—种。
5. 构成液体对所绕物体的阻力的两部分是:, 。
6. 从理论上看,探索液体运动基本规律的两种不同的途径是:,。
7. 在明渠恒定渐变流的能量方程式:J = J W+J V +J f中,J V的物理意义
是:。
8. 在水力学中,拉普拉斯方程解法最常用的有:, ,复变函数法,数值解法等。
9.加大下游水深的工程措施主要有:,使下游形成消能
池;使坎前形成消能池。
三计算题
1(15分).已知液体作平面流动的流场为:
2 2 _
u x = y - x +2x
u y = 2xy - 2y
试问:①此流动是否存在流函数",如存在,试求之;
②此流动是否存在速度势0,如存在,试求之。
2(15分).某分洪闸,底坎为曲线型低堰. 泄洪单宽流量q=1im/s,上下游堰高相等为2
米,下游水深h t=3米,堰前较远处液面到堰顶的高度为5米,若取?=0.903,试判断水跃形
式,并建议下游衔接的形式。(R=h c+q2/2g ?亿2)
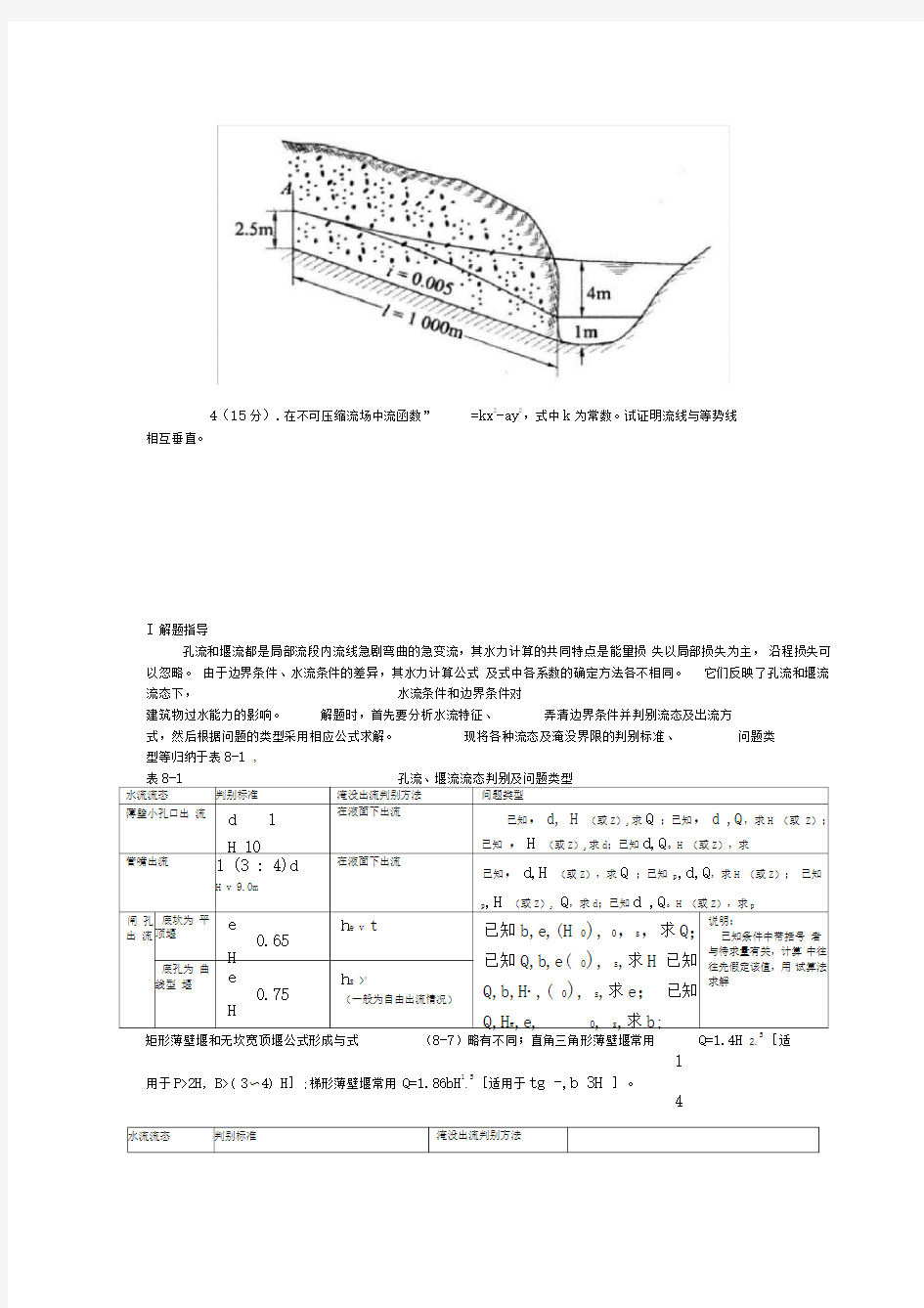
3(15分).设某河槽剖面地层情况如图示,左岸透水层中有地下水渗入河槽,河槽水深
1.0米,在距离河道1000米处的地下水深度为
2.5米,当此河槽下游修建水库后,此河槽
水位抬高了4米,若离左岸1000米处的地下水位不变,试问在修建水库后单位长度上渗入流量减少多少?
其中k=0.002cm/s ; s.i=h 2-h 1+2.3h o lg[(h 2-h o)/( h 1-h o)]
4(15分).在不可压缩流场中流函数”
=kx 2-ay 2
,式中k 为常数。试证明流线与等势线
相互垂直。
I 解题指导
孔流和堰流都是局部流段内流线急剧弯曲的急变流,其水力计算的共同特点是能量损 失以局部损失为主, 沿程损失可以忽略。 由于边界条件、水流条件的差异,其水力计算公式 及式中各系数的确定方法各不相同。 它们反映了孔流和堰流流态下,
水流条件和边界条件对
建筑物过水能力的影响。 解题时,首先要分析水流特征、
弄清边界条件并判别流态及出流方
式,然后根据问题的类型采用相应公式求解。
现将各种流态及淹没界限的判别标准、
问题类
型等归纳于表8-1 , 表
孔流、堰流流态判别及问题类型
矩形薄壁堰和无坎宽顶堰公式形成与式
(8-7)略有不同;直角三角形薄壁堰常用
Q=1.4H 2.[适
1
用于P >2H , B >( 3?4) H ];梯形薄壁堰常用 Q=1.86bH
1.
5
[适用于tg -,b 3H ]。
4
堰 流 底坎为 平
顶堰
e
一 > 0.65
H
薄壁堰 一 < 0.67
H
对矩形、梯形有 h s > 0 z/ R < 0.7
已知 b,(H 0 ),m,( , s ),求 Q ; 已知 Q,b,m,( , s ),求 H ;
已知 Q,m,(
), s , H ,求 b ; 已知 Q,b,H,
, s ,求 m
实用堰
0.67 < 莎 <2.5
不同剖面形状,判别界 限不同,可查有关册 克-奥 h s > 0 亠 Z Z
剖面
-- < ( ---- )k
R R
底坎为 曲线型 堰
e
一 > 0.75
H
宽顶堰
2.5 < — <
10
h s
——> 0.8
H 。
应该指出的是,由于本章各种系数计算的经验公式较多,在进行水力计算时应特主意 其适用条件是否相符,以免出错。
n 典型例题
[例8-1]甲、乙两水箱如例 8-1图。甲箱侧壁开有一直径为
100mm 的圆孔与乙箱相通。
甲箱底部为1.8X 1.8m 的正方形,水深 H 为2.5m 。孔口中心距箱壁的最近距离
h 为0.5m 。
当为恒定流时,问:①乙箱无水时,孔口的泄流量为多少?②乙箱水深 Hb=0.8m 时,孔口泄
流量为多少?③在甲箱外侧装一与孔口等径的
35cm 长圆柱形短管时,泄流量又为多少?若
管长为10cm,流量有何变化?当为管嘴出流时,管嘴内真空高度为若干?
解:
(1) 求乙箱无水时孔口的泄流量。孔口的
作用水头为
H H 1 h 2.0m,d/H
010
0.05 <0.1
2.0
乙箱无水,故为薄壁恒定小孔口自由出流。 孔口边缘距最近的边界距离
h=0.5m ,故h >3d=3
x 0.1=0.3m ,为完全完善收缩,取
0.62, 0.06,贝U
0.62 0.97 0.60
(2)
求当H 2=0.8m 时孔口的泄流量。 因此时为淹没出流, 且Z=H 1 —
H=2.5-0.8=1.7m 。
孔口位置、直径、边缘情况均未变,则 不变,故
Q A 2gZ 0
0.6 0.00785 ,19.6 1.7 0.0272m 3 / s
(3) 求甲箱外侧短管长 丨35cm, l 10cm 的泄流量及管嘴出流时的管内真宽度。 当I 35cm 时,其长度在(3?4) d=30?40cm 之间,为管嘴出流,
p p0而
0.82,于是自由出流时
,_,
2 2
因
A 箱 1.8 1.8 3.24m , A -d
4
故可忽略行近流速水头,即
H 0?H ,得
Q A 2gH 0
0.6 0.00785
空 0.12
2
0.00785( m ), A 箱
9.8 2.0 0.0295m 3/s
1
P
. 1 0.5
Q
淹没出流时
0.0403m 3 /s
| ---- 1
1 ' I
W x-i IM
0.82 0.00785 .19.6 2.0 p A,2gH0
Q p A 2gZ 0 0.82 0.00785 19.6 1.7 0.0372m 3/s
当I 10cm 时,I 3d 30cm ,故仍为孔口出流,泄流量与以上问题( 1)、(2)中的
结果完全相同。 以箱底为基准面,列 1-1、c-c 断面的能量方程, H 巳 a
0 0 g 2g
P c g 令H 。 2
a
o o
,
a
c 2g 1.0,整理上式得 A
A C
所以 P a P c g (1 2g H 。 p ._2gH o ——x 2gH
2
[T(1 h
P a P c
g
0.62, 0.06,代入上式,即得真空高度
2
h ■Pa —Pc [°^ (1 0.06) 1] 2.0 1.71m
g 0.62
显然,管嘴内形成一定的真空高度,增大了作用水头。故管嘴出流较孔口出流的流量大。 [例8-2]如例8-2图所示的密闭水箱,已知 H=2.5m , h=0.3m ,侧壁有孔径 d=20mm 的 圆形薄壁孔口,流量系数 0.60,P 。 0.1at o 求:①泄流开始时的泄流量;②当箱内水 深降至Hi=1.3m 时,欲保持泄流量不变, P 0应为多少米水柱高? (1)求泄流开始时的泄流量。由题意知,水流为薄壁孔口自 由出流 ■― — 0.02 0.0091 v 0.1,为小孔口。 H H 1 h 2.5 0.3 选取过孔口中心的水平面为基准面,对 断面列能量方程 以②代①, )1]H 。
将 p 0.82, 1-1、C-C H 1 2 也0 2g 2 a
2g 取 a c 1.0 o 因 A 箱 ? A c ,故 1
c ,故取 2
c 2g 2 丄0,则 2g 2g(H1 h 葺) P 0
2g(H1 h g ) c A
c
c
A A 『g(H1 h 弋)
