幂函数图象及其性质

幂函数的图像与性质
1、幂函数的定义
形如y=x α
(a ∈R )的函数称为幂函数,其中x 是自变量,α为常数
注:幂函数与指数函数有本质区别在于自变量的位置不同,幂函数的自变量在底数位置,而指数函数的自变量在指数位置。
例题、(1). 下列函数中不是幂函数的是( )
A .y =
B .3y x =
C .2y x =
D .1
y x -=
答案:C
例2.已知函数()()2531m f x m m x --=--,当 m 为何值时,()f x :
(1)是幂函数;(2)是幂函数,且是()0,+∞上的增函数;(3)是正比例函数;(4)是反比例函数;(5)是二次函数;
简解:(1)2m =或1m =-(2)1m =-(3)45m =-(4)2
5
m =-(5)1m =- 变式训练:已知函数()()
22
23
m m f x m m x
--=+,当
m 为何值时,()f x 在第一象限内它的
图像是上升曲线。
简解:220230
m m m m ?+>?
?-->??解得:()(),13,m ∈-∞-+∞
小结与拓展:要牢记幂函数的定义,列出等式或不等式求解。 2.幂函数的图像
幂函数y =x α的图象由于α的值不同而不同.
α的正负:α>0时,图象过原点和(1,1),在第一象限的图象上升;α<0,图象不过原点,在第一象限的图象下降,反之也成立;
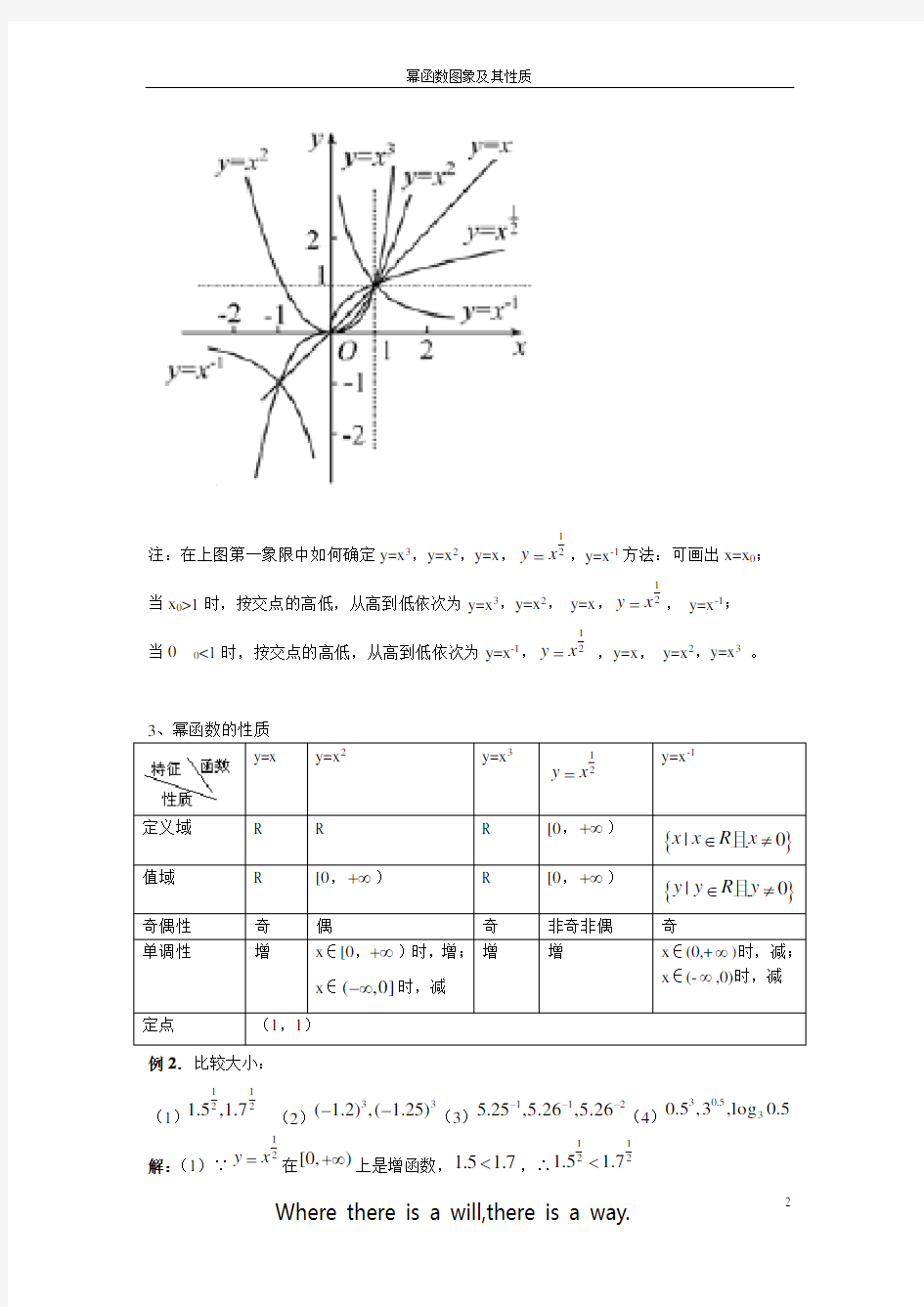
注:在上图第一象限中如何确定y=x 3
,y=x 2
,y=x ,12
y x =,y=x -1方法:可画出x=x 0; 当x 0>1时,按交点的高低,从高到低依次为y=x 3,y=x 2, y=x ,12
y x =, y=x -1; 当0 ,12 y x = ,y=x , y=x 2,y=x 3 。 例2.比较大小: (1)1 122 1.5,1.7 (2)33( 1.2),( 1.25)--(3)112 5.25,5.26,5.26---(4) 30.530.5,3,log 0.5 解:(1)∵1 2 y x =在[0,)+∞上是增函数,1.5 1.7<,∴1122 1.5 1.7< (2)∵3y x =在R 上是增函数, 1.2 1.25->-,∴33 ( 1.2)( 1.25)->- (3)∵1y x -=在(0,)+∞上是减函数,5.25 5.26<,∴11 5.25 5.26-->; ∵ 5.26x y =是增函数,12->-,∴12 5.26 5.26-->; 综上,112 5.25 5.26 5.26--->> (4)∵300.51<<,0.531>,3log 0.50<,∴30.53log 0.50.53<< 5.幂函数的性质及其应用 幂函数y =x α有下列性质:(1)单调性:当α>0时,函数在(0,+∞)上单调递增;当α<0时,函数在(0,+∞)上单调递减.(2)奇偶性:幂函数中既有奇函数,又有偶函数,也有非奇非偶函数,可以用函数奇偶性的定义进行判断. 例3.已知幂函数2 23 m m y x --=(m Z ∈)的图象与x 轴、y 轴都无交点,且关于原点对称, 求m 的值. 解:∵幂函数223 m m y x --=(m Z ∈)的图象与x 轴、y 轴都无交点, ∴2 230m m --≤,∴13m -≤≤; ∵m Z ∈,∴2 (23)m m Z --∈,又函数图象关于原点对称, ∴2 23m m --是奇数,∴0m =或2m =. 例7.已知点在幂函数()f x 的图象上,点124? ?- ?? ?,,在幂函数()g x 的图象上.问当x 为何值时有:(1)()()f x g x >;(2)()()f x g x =;(3)()()f x g x <. 变式:已知幂函数f(x)=x 3 22 --m m (m ∈Z )为偶函数,且在区间(0,+∞)上是单调减函数. (1)求函数f(x); (2)讨论F (x )=a ) ()(x xf b x f -的奇偶性. 6.规律方法 (1).幂函数y =x α(α=0,1)的图象 (2).幂函数(,,,a q q y x a p q N p p *== ∈为最简分式) 的图象 例1.概念:一般地,我们把形如 的函数称为幂函数,其中 是自变量, 是常数;注意:幂函数与指数函数的区别. 2.性质: (1)幂函数的图象都过点 ;任何幂函数都不过 象限; (2)当0a >时,幂函数在[0,)+∞上 ;当0a <时,幂函数在(0,)+∞上 ; (3)当2,2a =-时,幂函数是 ;当1 1,1,3,3 a =-时,幂函数是 . 例1、右图为幂函数y x α=在第一象限的图 像,则,,,a b c d 的大小关系是 ( ) ()A a b c d >>> ()B b a d c >>> ()C a b d c >>> ()D a d c b >>> 解:取12 x =, 由图像可知:11112222c d b a ???????? >>> ? ? ? ????????? , a b d c ?>>>,应选()C . 综合训练: 1.在函数220 31,3,,y y x y x x y x x = ==-=中,幂函数的个数为 ( ) A .0 B .1 C .2 D .3 2、幂函数的图象都经过点( ) A .(1,1) B .(0,1) C .(0,0) D .(1,0) 3、幂函数2 5 -=x y 的定义域为( ) A .(0,+∞) B .[0,+∞) C .R D .(-∞,0)U (0,+∞) 4.若幂函数()a f x x =在()0,+∞上是增函数,则 ( ) A .a >0 B .a <0 C .a =0 D .不能确定 6.若幂函数()1 m f x x -=在(0,+∞)上是减函数,则 ( ) A .m >1 B .m <1 C .m =l D .不能确定 9、若四个幂函数y =a x ,y =b x ,y =c x ,y =d x 在同一坐标系中的图象如右图,则a 、b 、c 、 d 的 大 小 关 系 是 ( ) A 、d >c >b >a B 、a >b >c >d C 、d >c >a >b D 、a >b >d >c b c 10、当x ∈(1,+∞)时,函数)y =a x 的图象恒在直线y =x 的下方,则a 的取值范围是 A 、a <1 B 、0<a <1 C 、a >0 D 、a <0 二、填空题: 12、若2 1 ) 1(-+a <2 1) 23(--a ,则a 的取值范围是____; 13.函数2 3- =x y 的定义域为___________. 三、解答题: 17下面六个幂函数的图象如图所示,试建立函数与图象之间的对应关系. . 6543212 1 323 23123---======x y x y x y x y x y x y );();()(;);();()( (A ) (B ) (C ) (D ) (E ) (F ) 四:方向预测、胜利在望 1—5 ADDDC ; 6—10 AADDA ; 11—15 CADDB. 1.(A )函数4 1lg )(--=x x x f 的定义域为( ) A .(1,4) B .[1,4) C .(-∞,1)∪(4,+∞) D .(-∞,1]∪(4,+∞) 2.(A )以下四个数中的最大者是( ) (A) (ln2)2 (B) ln(ln2) (C) ln 2 (D) ln2 5.(B )设f (x )= 12 32,2, log (1),2, x e x x x -?2的解集为( ) (A)(1,2)?(3,+∞) (B)(10,+∞) (C)(1,2)? (10 ,+∞) (D)(1,2) 6.(A )设2log 3P =,3log 2Q =,23log (log 2)R =,则( ) A.R Q P << B.P R Q << C.Q R P << D.R P Q << 7.(A)已知c a b 21212 1log log log <<,则( ) A .c a b 222>> B .c b a 222>> C .a b c 222>> D .b a c 222>> 9.(A ) 函数y =的定义域是:( ) A [1,)+∞ B 23(,) +∞ C 23[,1] D 23(,1] 10.(A)已知函数kx y x y ==与4 1log 的图象有公共点A ,且点A 的横坐标为2,则k ( ) A .41- B .41 C .2 1- D .21 11.(B )若函数的图象经过第二且)10(1)(≠>-+=a a b a x f x 、三、四象限,则一定 有( ) A .010><>b a 且 C .010<< D .01<>b a 且 14.(A )已知x x f 26log )(=,那么)8(f 等于( ) (A ) 3 4 (B )8 (C )18 (D ) 2 1 15.(B )函数y =lg|x| ( ) A .是偶函数,在区间(-∞,0)上单调递增 B .是偶函数,在区间(-∞,0)上单调递减 C .是奇函数,在区间(0,+∞)上单调递增 D .是奇函数,在区间(0,+∞)上单调递减 16.(A )函数3) 4lg(--= x x y 的定义域是 ____________________________. 18.(A )设,0.(),0. x e x g x lnx x ?≤=?>? 则1 (())2g g =__________ 19.(B )若函数f(x) = 1222--+a ax x 的定义域为R ,则a 的取值范围为___________. 20.(B)若函数)2(log )(2 2a a x x x f ++=是奇函数,则a = . 16. (-∞, 3)?(3,4) 18. 21 19.[-1,0] 20. 2 2 指数函数、对数函数、幂函数的图像与性质 (一)指数与指数函数 1 .根式 ( 1 )根式的概念 根式的概念 符号表示 备注 如果 x n a , 那么 x 叫做 a 的 n 次方根 n 1且 n N 当 n 为奇数时 ,正数的 n 次方根是一个正数 , 负数的 n 次 n a 零的 n 次方根是零 方根是一个负数 当 n 为偶数时 , 正数的 n 次方根有两个 , 它们互为相反 n a ( a 0) 负数没有偶次方根 数 ( 2 ).两个重要公式 a n 为奇数 ① n a n a( a 0) ; | a | 0) n 为偶数 a(a ② (n a ) n a (注意 a 必须使 n a 有意义)。 2 .有理数指数幂 ( 1 )幂的有关概念 m n a m (a ①正数的正分数指数幂 : a n 0, m 、 n N ,且 n 1) ; m 1 1 ②正数的负分数指数幂 : a n 0, m 、 n N , 且 n 1) m (a a n n a m ③0 的正分数指数幂等于 0,0 的负分数指数幂没有意义 . 注: 分数指数幂与根式可以互化,通常利用分数指数幂进行根式的运算。 ( 2 )有理数指数幂的性质 ①a r a s =a r+s (a>0,r 、 s ∈ Q); ②(a r )s =a rs (a>0,r 、 s ∈ Q); ③(ab) r =a r b s (a>0,b>0,r ∈Q);. 3.指数函数的图象与性质 y=a x a>10 幂函数的图像与性质 Prepared on 22 November 2020 【知识结构】 1.有理数指数幂 (1)幂的有关概念 ①正数的正分数指数幂 :0,,1)m n a a m n N n *=>∈>、且; ②正数的负分数指数幂 : 10,,1)m n m n a a m n N n a -*= = >∈>、且 ③0的正分数指数幂等于0,0的负分数指数幂没有意义. 注:分数指数幂与根式可以互化,通常利用分数指数幂进行根式的运算。 (2)有理数指数幂的性质 ①a r a s =a r+s (a>0,r 、s ∈Q );②(a r )s =a rs (a>0,r 、s ∈Q ); ③(ab)r =a r b s (a>0,b>0,r ∈Q );. 例2 (1)计算:25 .021 21 32 5.032 0625.0])32.0()02.0()008.0()94 5()833[(÷?÷+---; (2)化简:533233 23 23 3 23 134)2(248a a a a a b a a ab b b a a ??? -÷++-- 变式:(2007执信A )化简下列各式(其中各字母均为正数): (1) ;)(6 5 3 121211 3 2 b a b a b a ????- -(2).)4()3(6 521 3 32121231----?÷-??b a b a b a (3) 100.2563 71.5()86-?-+(三)幂函数 1、幂函数的定义 形如y=x α(a ∈R )的函数称为幂函数,其中x 是自变量,α为常数 注:幂函数与指数函数有本质区别在于自变量的位置不同,幂函数的自变量在底数位置,而指数函数的自变量在指数位置。 例1.下列函数中不是幂函数的是( ) A .y = B .3y x = C .2y x = D .1 y x -= 例2.已知函数()()2531m f x m m x --=--,当 m 为何值时,()f x : (1)是幂函数;(2)是幂函数,且是()0,+∞上的增函数; (3)是正比例函数;(4)是反比例函数;(5)是二次函数; 变式 已知幂函数2 223(1)m m y m m x --=--,当(0)x ∈+,∞时为减函数,则幂函数 y =_______. 2.幂函数的图像 幂函数y =x α的图象由于α的值不同而不同. α的正负:α>0时,图象过原点和(1,1),在第一象限的图象上升; α<0时,图象不过原点,在第一象限的图象下降,反之也成立; 3、幂函数的性质 例3.比较大小: 指对幂函数图像及其性质 1. 已知函数()() 123,2,log 1,2,x e x f x x x -?)的图象如图所示,则函数()()log a g x x b =-的图象大致是( ). A . B . C . D . 5. e 是自然对数的底数,若() 1,1x e -∈,ln a x =,12x b ??= ???,x c e =,则( ) A .b c a >> B .a b c >> C .c b a >> D .c a b >> 6. 已知()f x 是周期为2的奇函数,当01x <<时,12 ()log f x x =,设6()5a f =,3()2b f =,5()2c f =,则,,a b c 的大小关系为( ). A. a b c << B. c b a << C. c a b << D. b a c << 7. 设,x y 为负实数且23x y =,则下列说法正确的是( ) A .32y x = B .32y x < C .23x y < D .以上都不对 8. 设a ,b ,c 均为正数,且12 2log a a =,121()log 2b b =,21()log 2c c =,则a ,b ,c 的大小关系为( ). A. c a b << B. c b a << C. a b c << D. b a c << 9. 若23a b ==6,则4a -=___;11a b +=___ 10. 设37,52a ??∈-??? ?,则使函数a y x =的定义域为R 且为奇函数的所有α值为__________. 幂函数 分数指数幂 正分数指数幂的意义是:m n m n a a =(0a >,m 、n N ∈,且1n >) 负分数指数幂的意义是:m n n m a a - = (0a >,m 、n N ∈,且1n >) 一、幂函数的定义 一般地,形如 y x α =(x ∈R )的函数称为幂孙函数,其中x 是自变量,α是常数.如 112 3 4 ,,y x y x y x -===等都是幂函数,幂函数与指数函数,对数函数一样,都是基本初等函数. 二、幂函数的图像 幂函数n y x =随着n 的不同,定义域、值域都会发生变化,可以采取按性质和图像分类记忆的方法.熟练掌握n y x =,当11 2,1,,,323 n =±±± 的图像和性质,列表如下. 从中可以归纳出以下结论: ① 它们都过点()1,1,除原点外,任何幂函数图像与坐标轴都不相交,任何幂函数图像都不过第四象限. ② 11 ,,1,2,332a =时,幂函数图像过原点且在[)0,+∞上是增函数. ③ 1 ,1,22 a =---时,幂函数图像不过原点且在()0,+∞上是减函数. ④ 任何两个幂函数最多有三个公共点. 三、幂函数基本性质 (1)所有的幂函数在(0,+∞)都有定义,并且图象都过点(1,1); (2)α>0时,幂函数的图象都通过原点,并且在[0,+∞]上,是增函数 (3)α<0时,幂函数的图象在区间(0,+∞)上是减函数. 规律总结 1.在研究幂函数的性质时,通常将分式指数幂化为根式形式,负整指数幂化为分式形式再去进行讨论; 2.对于幂函数y =αx ,我们首先应该分析函数的定义域、值域和奇偶性,由此确定图象的位置,即所在象限,其次确定曲线的类型,即α<0,0<α<1和α>1三种情况下曲线的基本形状,还要注意α=0,±1三个曲线的形状;对于幂函数在第一象限的图象的大致情况可以用口诀来记忆:“正抛负双,大竖小横”,即α>0(α≠1)时图象是抛物线型;α<0时图象是双曲线型;α>1时图象是竖直抛物线型;0<α<1时图象是横卧抛物线型. 四、幂函数的应用 题型一.幂函数的判断 例1.在函数22031 ,3,,y y x y x x y x x ===-=中,幂函数的个数为 ( ) A .0 B .1 C .2 D .3 练1.下列所给出的函数中,是幂函数的是( ) 【知识结构】 1.有理数指数幂 (1)幂的有关概念 ①正数的正分数指数幂 :0,,1)m n a a m n N n *=>∈>、且; ②正数的负分数指数幂 : 1 0,,1)m n m n a a m n N n a -*==>∈>、且 ③0的正分数指数幂等于0,0的负分数指数幂没有意义. 注:分数指数幂与根式可以互化,通常利用分数指数幂进行根式的运算。 (2)有理数指数幂的性质 ①a r a s =a r+s (a>0,r 、s ∈Q );②(a r )s =a rs (a>0,r 、s ∈Q ); ③(ab)r =a r b s (a>0,b>0,r ∈Q );. 例2 (1)计算:25 .021 21325.0320625.0])32.0()02.0()008.0()945()833[(÷?÷+---; (2)化简:533233232332 3134)2(248a a a a a b a a ab b b a a ???-÷++-- 变式:(2007执信A )化简下列各式(其中各字母均为正数): (1) ;)(653 12121 132b a b a b a ????--(2).)4()3(6521332121231----?÷-??b a b a b a (3) 1 00.256371.5()86-?-+ (三)幂函数 1、幂函数的定义 形如y=x α(a ∈R )的函数称为幂函数,其中x 是自变量,α为常数 注:幂函数与指数函数有本质区别在于自变量的位置不同,幂函数的自变量在底数位置,而指数函数的自变量在指数位置。 例1.下列函数中不是幂函数的是( ) A .y x = B .3y x = C .2y x = D .1y x -= 例2.已知函数()()2531m f x m m x --=--,当 m 为何值时,()f x : (1)是幂函数;(2)是幂函数,且是()0,+∞上的增函数; (3)是正比例函数;(4)是反比例函数;(5)是二次函数; 变式 已知幂函数2 223(1)m m y m m x --=--,当(0)x ∈+,∞时为减函数,则幂函数y =_______. 2.幂函数的图像 幂函数y =x α的图象由于α的值不同而不同. α的正负:α>0时,图象过原点和(1,1),在第一象限的图象上升; α<0时,图象不过原点,在第一象限的图象下降,反之也成立; 【知识结构】 1 ?有理数指数幕 (1)幕的有关概念 m ①正数的正分数指数幕:a n v'a m (a 0,m> n N ,且n 1); (三)幕函数 1、幕函数的定义 形如y=x " (a € R )的函数称为幕函数, m 1 1 a n m / ----- (a m n a a ②正数的负分数指数幕 0,m 、n N ,且n 1) ③0的正分数指数幕等于0,0的负分数指数幕没有意义 注:分数指数幕与根式可以互化,通常利用分数指数幕进行根式的运算 (2)有理数指数幕的性质 ①a f a s =a r+s (a>0,r 、s € Q ②(a r )s =a rs (a>0,r 、s € Q); ③(ab)r =a r b s (a>0,b>0,r € Q);. 例2 (1)计算: 3 "3 4 o 5 [(38)3(56) . 2 1 1 (0.008) 3 (0.02) ' (0.32円 0.06250.25 4 1 a 3 8a 3b 2 2 (2)化简:4b 3 23 ab a 3 (a 3 23 b) . a 3 a 2 a 引Ja Va 变式: (1) (2007执信A )化简下列各式(其中各字母均为正数) 2) 1 2 1 b 2 ( 3a?b 1) (4a? b 予. 其中x是自变量,a为常数 注:幕函数与指数函数有本质区别在于自变量的位置不同,幕函数的自变量在底数位置,而指数函数的自变量在指数位置。 例1.下列函数中不是幕函数的是() A. y Vx B. y X3 C y 2x D. y X1 例2.已知函数f x m2m 1 x 5m 3,当m为何值时,f x : (1)是幕函数;(2)是幕函数,且是0, 上的增函数; (3)是正比例函数;(4)是反比例函数;(5)是二次函数; 变式已知幕函数y (m2 m 1)x m 2m 3,当x (0,g)时为减函数,则幕函数 y _______ - 2. 幕函数的图像 幕函数y= x a的图象由于a的值不同而不同. a的正负:a> 0时,图象过原点和(1,1),在第一象限的图象上升; aV0时,图象不过原点,在第一象限的图象下降,反之也成立; 幂函数的图像与性质 (三)幂函数 1、幂函数的定义 形如y=x α(a ∈R )的函数称为幂函数,其中x 是自变量,α为常数 注:幂函数与指数函数有本质区别在于自变量的位置不同,幂函数的自变量在底数位置,而指数函数的自变量在指数位置。 例1.下列函数中不是幂函数的是( ) A .y x = B .3y x = C .2y x = D .1 y x -= 例2.已知函数()()2531m f x m m x --=--,当 m 为何值时,()f x : (1)是幂函数;(2)是幂函数,且是()0,+∞上的增函数; (3)是正比例函数;(4)是反比例函数;(5)是二次函数; 变式 已知幂函数2 223(1)m m y m m x --=--,当(0)x ∈+,∞时为减函数,则幂函数 y =_______. 2.幂函数的图像 幂函数y =x α的图象由于α的值不同而不同. α的正负:α>0时,图象过原点和(1,1),在第一象限的图象上升; α<0时,图象不过原点,在第一象限的图象下降,反之也成立; 3、幂函数的性质 y=x y=x 2 y=x 3 12 y x = y=x -1 定义域 R R R [0,+∞) {}|0x x R x ∈≠且 值域 R [0,+∞) R [0,+∞) {}|0y y R y ∈≠且 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增 x ∈[0,+∞)时,增; x ∈(,0]-∞时,减 增 增 x ∈(0,+∞)时,减; x ∈(-∞,0)时,减 定点 (1,1) 例3.比较大小: (1)112 2 1.5,1.7 (2)33( 1.2),( 1.25)--(3)112 5.25,5.26,5.26---(4)30.530.5,3,log 0.5 4.幂函数的性质及其应用 幂函数y =x α有下列性质: (1) 单调性:当α>0时,函数在(0,+∞)上单调递增; 当α<0时,函数在(0,+∞)上单调递减. (2)奇偶性:幂函数中既有奇函数,又有偶函数,也有非奇非偶函数,可以用函数奇偶性的定义进行判断. 例4.已知幂函数2 23 m m y x --=(m Z ∈)的图象与x 轴、y 轴都无交点,且关于 原点对称,求m 的值. 幕函数的图像与性质 1幕函数的定义 形如y=x "(a € R )的函数称为幕函数,其中 x 是自变量,a 为常数 注:幕函数与指数函数有本质区别在于自变量的位置不同, 幕函数的自变量在底数位置, 而 指数函数的自变量在指数位置。 例题、(1).下列函数中不是幕函数的是( ) A . y 仮 B . y x 3 c . y 2x D . y x 1 答案:C 例2.已知函数f x m 2 m 1 x 5m 3,当m 为何值时,f x 图像是上升曲线。 (1)是幕函数; (2)是幕函数,且是 0, 上的增函数;(3)是正比例函数;(4)是反 比例函数; (5) 是二次函数; 简解:(1) (2) (3) m 4 (4) m 5 (5) m 1 变式训练: 已知函数f x m 2 2m m 为何值时, 在第一象限内它的 2 小 简解:m m 0 2 m 2m 3 解得:m 0 U 3, 小结与拓展:要牢记幕函数的定义,列出等式或不等式求解。 2.幕函数的图像 幕函数y = x a 的图象由于a 的值不同而不同. a 的正负:a> 0时,图象过原点和(1,1),在第一象限的图象上升; 在第一象限的图象下降,反之也成立; aV 0,图象不过原点, 1 注:在上图第一象限中如何确定 y=x 3, y=x 2, y=x , y x 2 , y=x -1方法:可画出x=x o ; 当x o >l 时,按交点的高低,从高到低依次为 y=x 3, y=x 2, 当0 【课题】 幂函数的性质与图像 【执教者】:关雅南(上海师范大学附属外国语中学) 【教学目标】:知识和技能:理解幂函数的概念,掌握幂函数的性质与图像并能 简单应用。 过程和方法:通过研究性质培养学生分析归纳的思维能力,体会 从特殊到一般的研究问题的数学方法和数形结合 的数学思想。 情感、态度和价值观:培养学生积极探究、合作交流的学习品质,激发学 生的学习兴趣和探究热情。 【教学重点】:幂函数的性质与图像 【教学难点】:幂函数性质与图像特征的归纳 【教学过程】: 一. 创设情境,引入新知 回顾初中阶段所学的正比例函数如y=x,反比例函数如y=x 1即y=1-x ,二次函数如y=2x ,另外正方体的体积y 关于边长x 的函数解析式为y=3x ,正方形的边长y 关于面积x 的函数关系式为y=x 即y=21x ,分析这些函数有什么共同特征? 解析式右边为幂的形式,底数为自变量,系数为1. 这些函数可统一写成y=k x 的形式,引出幂函数的定义。 二. 幂函数定义 一般地,函数y=k x (k 为常数,k ∈Q )叫做幂函数(power function ) 概念巩固:判断下列函数是否为幂函数? (1) y=x 3.0 (2)y=21 _x (3)y=3x +x (4) y=23x 三. 研究特殊的幂函数的性质与图像的方法 例题:研究函数y=21 _x 的定义域、奇偶性和单调性,并且作出它的图像。 (师生共同探究此幂函数性质,课件演示利用描点法作出的函数图像,并 观察此幂函数性质在图像上的体现)。 自主探究: 研究函数y=32x 的定义域、奇偶性、单调性和最大值或最小值。 (在课堂练习单上独立完成,投影演示,师生共同评价) 四. 合作探究一般的幂函数性质与图像特征 1.教师演示:在同一直角坐标系分别演示幂函数y=21_x 、 y=2 x 和y=31_x 的图像,认真观察图像,体会其中蕴含的函数性质。 2.小组讨论: 归纳幂函数(k 0)的性质和图像特征 (1) 在第一象限单调性如何? (2) 有无公共点? (3) 图像与坐标轴的位置关系? (4) 图像的象限分布有何特点?特点由什么确定? 3.类比探究:在同一直角坐标系分别演示幂函数y=21x 、 y=32x 和y=31x 的图 像,幂函数y=23x 、 y=2x 和y=3x 的图像,类比探究当0 k 1 和k 1时幂函数性质 五. 课堂巩固、简单应用 练习:比较下列两组数的大小 ①253_________251.3 ② (-0.96) 31__________ (-0.95)31_ 六. 课堂小结 今天的学习内容和方法有哪些?你有哪些收获? 七. 布置作业:课本81页:习题4.1 写一篇题为《幂函数研究方法初探》的数学小论文 (一)指数与指数函数 1.根式 (1)根式的概念 (2).两个重要公式 ① ? ? ? ? ? ? ? ? < - ≥ = = )0 ( )0 ( | | a a a a a a a n n; ②a a n n= ) ((注意a必须使n a有意义)。 2.有理数指数幂 (1)幂的有关概念 ①正数的正分数指数幂:0,,1) m n m n a a a m n N n * =>∈> 、且; ②正数的负分数指数幂: 1 0,,1) m n m n m n a a m n N n a a - * ==>∈> 、且 ③0的正分数指数幂等于0,0的负分数指数幂没有意义. 注:分数指数幂与根式可以互化,通常利用分数指数幂进行根式的运算。 (2)有理数指数幂的性质 ①a r a s=a r+s(a>0,r、s∈Q); ②(a r)s=a rs(a>0,r、s∈Q); ③(ab)r=a r b s(a>0,b>0,r∈Q);. 3.指数函数的图象与性质 y=a x a>1 0 图象 定义域R 值域(0,+∞) 性质(1)过定点(0,1) (2)当x>0时,y>1; x<0时,0 课件6幕函数图象及性质 课件编号:AB I -2-3-1. 课件名称:幕函数图象及性质? 课件运行环境:几何画板4.0以上版本. 课件主要功能:配合教科书“ 2.3幕函数”的教学.利用几何画板绘制函数图象的功能,绘制出幕函数的图象,再利用幕函数的图象研究函数的性质. 课件制作过程: (1)新建画板窗口.单击【Graph](图表)菜单中的【Define Coordinate System!(建立直角坐标系),建立直角坐标系.选中原点,按Ctrl + K,给原点加注标签A,并用【文本]工具把标签改为O. (2)单击【Graph]菜单的【Plot New Function](绘制函数图象),弹出“New Function”函数式编辑器,编辑函数f (x)= x,单击【OK]后画出函数f (x) 1 , , _ 2 3 —_ 1 =x的图象.同法编辑函数g (x)= x,h (x)= x,q(x)=x2和函数r(x)二一的 x 图象.选中函数图象,单击【Display](显示)菜单中的【Line Width](线型)中的【Thick](粗线).把上述图象设置成粗线,单击【Display](显示)菜单中的【Color](颜色)的选择各种不同的颜色给每一个函数图象着色,如图1. 图1 (3)再选中直线f (x) = x,单击【Edit](编辑)菜单,选择【Action Buttons] (操作类按钮),单击【Hide/Show](隐藏/显示),此时屏幕上出现【Hide Function Plot](隐藏对象)按钮,选择【文本工具】,双击【Hide Function Plot】按钮, 出现对话框,将其中的【Label](标签)改为“ f (x)= x”,再单击【确定】?此时,单击“f (x)二x”按钮就会隐藏或显示直线f (x)二x ?用同样的方法制作 1 【Hide Function Plot】按钮g (x)= x2,h(x)=x3,q(x)=x2和r(x)二-,如图 x 2. (4)单击【File】(文件)菜单的【Document Options】(文档选项)对话框,将【Page Namd (页面名称)改为“画图象”,单击【0K】. (5)单击【File】(文件)菜单的【Document Options】(文档选项)对话框, 单击【Add Page](增加页),单击【Blank Pagd (空白页),将页面名称改为“ g 2” (X)= x ? (6)单击【Graph】菜单的【Plot New Function】(绘制函数图象),弹出 “New Function”函数式编辑器,在对话框内依次单击x,A,2,单击【OK】后画出函 指数函数、对数函数、幂函数的图像与性质 (一)指数与指数函数 1.根式 (1)根式的概念 (2).两个重要公式 ①?? ??????<-≥==)0()0(||a a a a a a a n n ; ②a a n n =)((注意a 必须使n a 有意义)。 2.有理数指数幂 (1)幂的有关概念 ①正数的正分数指数幂:0,,1)m n a a m n N n *=>∈>、且; ②正数的负分数指数幂: 10,,1)m n m n a a m n N n a - *= = >∈>、且 ③0的正分数指数幂等于0,0的负分数指数幂没有意义、 注:分数指数幂与根式可以互化,通常利用分数指数幂进行根式的运算。 (2)有理数指数幂的性质 ①a r a s =a r+s (a>0,r 、s ∈Q ); ②(a r )s =a rs (a>0,r 、s ∈Q ); ③(ab)r =a r b s (a>0,b>0,r ∈Q );、 3.指数函数的图象与性质 n 为奇数 n 为偶数 图象 定义域R 值域(0,+∞) 性质(1)过定点(0,1) (2)当x>0时,y>1; x<0时,0 【知识结构】 1.有理数指数幂 (1)幂的有关概念 ①正数的正分数指数幂 :0,,1)m n a a m n N n *=>∈>、且; ②正数的负分数指数幂 : 10,,1)m n m n a a m n N n a -*= = >∈>、且 ③0的正分数指数幂等于0,0的负分数指数幂没有意义. 注:分数指数幂与根式可以互化,通常利用分数指数幂进行根式的运算。 (2)有理数指数幂的性质 ①a r a s =a r+s (a>0,r 、s ∈Q);②(a r )s =a rs (a>0,r 、s ∈Q); ③(ab)r =a r b s (a>0,b>0,r ∈Q);. 例2 (1)计算:25 .021 21 3 2 5 .032 0625.0])32.0()02.0()008.0()945()833[(÷?÷+---; (2)化简:533233 23 23 3 23 134)2(248a a a a a b a a ab b b a a ??? -÷++-- 变式:(2007执信A )化简下列各式(其中各字母均为正数): (1) ;)(6 5 3 121211 3 2 b a b a b a ????- -(2).)4()3(6 521 3 32121231----?÷-??b a b a b a (3) 100.2563 71.5()86-?-+- (三)幂函数 1、幂函数的定义 形如y=x α(a ∈R )的函数称为幂函数,其中x 是自变量,α为常数 注:幂函数与指数函数有本质区别在于自变量的位置不同,幂函数的自变量在底数位置,而指数函数的自变量在指数位置。 例1.下列函数中不是幂函数的是( ) A .y x = B .3y x = C .2y x = D .1 y x -= 例2.已知函数()()2531m f x m m x --=--,当 m 为何值时,()f x : (1)是幂函数;(2)是幂函数,且是()0,+∞上的增函数; (3)是正比例函数;(4)是反比例函数;(5)是二次函数; 变式 已知幂函数2 223(1)m m y m m x --=--,当(0)x ∈+,∞时为减函数,则幂函数 y =_______. 2.幂函数的图像 幂函数y =x α的图象由于α的值不同而不同. α的正负:α>0时,图象过原点和(1,1),在第一象限的图象上升; α<0时,图象不过原点,在第一象限的图象下降,反之也成立; 幂函数的图像与性质 1、幂函数的定义 形如y=x α (a ∈R )的函数称为幂函数,其中x 是自变量,α为常数 注:幂函数与指数函数有本质区别在于自变量的位置不同,幂函数的自变量在底数位置,而指数函数的自变量在指数位置。 例题、(1). 下列函数中不是幂函数的是( ) A .y = B .3y x = C .2y x = D .1 y x -= 答案:C 例2.已知函数()()2531m f x m m x --=--,当 m 为何值时,()f x : (1)是幂函数;(2)是幂函数,且是()0,+∞上的增函数;(3)是正比例函数;(4)是反比例函数;(5)是二次函数; 简解:(1)2m =或1m =-(2)1m =-(3)45m =-(4)2 5 m =-(5)1m =- 变式训练:已知函数()() 22 23 m m f x m m x --=+,当 m 为何值时,()f x 在第一象限内它的 图像是上升曲线。 简解:220230 m m m m ?+>? ?-->??解得:()(),13,m ∈-∞-+∞ 小结与拓展:要牢记幂函数的定义,列出等式或不等式求解。 2.幂函数的图像 幂函数y =x α的图象由于α的值不同而不同. α的正负:α>0时,图象过原点和(1,1),在第一象限的图象上升;α<0,图象不过原点,在第一象限的图象下降,反之也成立; 注:在上图第一象限中如何确定y=x 3 ,y=x 2 ,y=x ,12 y x =,y=x -1方法:可画出x=x 0; 当x 0>1时,按交点的高低,从高到低依次为y=x 3,y=x 2, y=x ,12 y x =, y=x -1; 当0 指数函数对数函数幂函数的图像和性质知识点 总结 Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】 (一)指数与指数函数 1.根式 (1)根式的概念 (2).两个重要公式 ①????????<-≥==)0()0(||a a a a a a a n n ; ②a a n n =)((注意a 必须使n a 有意义)。 2.有理数指数幂 (1)幂的有关概念 ①正数的正分数指数幂:0,,1)m n a a m n N n *=>∈>、且; ②正数的负分数指数幂:10,,1)m n m n a a m n N n a -*= = >∈>、且 ③0的正分数指数幂等于0,0的负分数指数幂没有意义. 注:分数指数幂与根式可以互化,通常利用分数指数幂进行根式的运算。 (2)有理数指数幂的性质 ①a r a s =a r+s (a>0,r 、s ∈Q); ②(a r )s =a rs (a>0,r 、s ∈Q); ③(ab)r =a r b s (a>0,b>0,r ∈Q);. 3.指数函数的图象与性质 n 为奇数 n 为偶 数 注:如图所示,是指数函数(1)y=a x ,(2)y=b x,(3),y=c x (4),y=d x 的图象,如何确定底数a,b,c,d 与1之间的大小关系? 提示:在图中作直线x=1,与它们图象交点的纵坐标即为它们各自底数的值,即c 1>d 1>1>a 1>b 1,∴c>d>1>a>b 。即无论在轴的左侧还是右侧,底数按逆时针方向变大。 (二)对数与对数函数 1、对数的概念 (1)对数的定义 如果(01)x a N a a =>≠且,那么数x 叫做以a 为底,N 的对数,记作log N a x =,其中a 叫做对数的底数,N 叫做真数。 (2 2(1)对数的性质(0,1a a >≠且):①1 log 0a =,②log 1a a =,③log N a a N =, ④log N a a N =。 (2)对数的重要公式: ①换底公式:log log (,1,0)log N N a b b a a b N =>均为大于零且不等于; ②1 log log b a a b = 。 (3)对数的运算法则: 如果0,1a a >≠且,0,0M N >>那么 ①N M MN a a a log log )(log +=; ②N M N M a a a log log log -=; ③)(log log R n M n M a n a ∈=; (一)指数与指数函数 1.根式 (1)根式的概念 (2).两个重要公式 ①?? ??????<-≥==)0()0(||a a a a a a a n n ; ②a a n n =)((注意a 必须使n a 有意义)。 2.有理数指数幂 (1)幂的有关概念 ①正数的正分数指数幂:0,,1)m n m n a a a m n N n *=>∈>、且; ②正数的负分数指数幂: 10,,1)m n m n m n a a m n N n a a - *= = >∈>、且 ③0的正分数指数幂等于0,0的负分数指数幂没有意义、 注:分数指数幂与根式可以互化,通常利用分数指数幂进行根式的运算。 (2)有理数指数幂的性质 ①a r a s =a r+s (a>0,r 、s ∈Q ); ②(a r )s =a rs (a>0,r 、s ∈Q ); ③(ab)r =a r b s (a>0,b>0,r ∈Q );、 3.指数函数的图象与性质 y=a x a>1 0 图象 定义域R 值域(0,+∞) 性质(1)过定点(0,1) (2)当x>0时,y>1; x<0时,0 (一)指数与指数函数 1.根式 (1)根式的概念 (2).两个重要公式 ①?? ??????<-≥==)0()0(||a a a a a a a n n ; ②a a n n =)((注意a 必须使n a 有意义)。 2.有理数指数幂 (1)幂的有关概念 ①正数的正分数指数幂:0,,1)m n m n a a a m n N n *=>∈>、且; ②正数的负分数指数幂: 10,,1)m n m n m n a a m n N n a a - *= = >∈>、且 ③0的正分数指数幂等于0,0的负分数指数幂没有意义。 注:分数指数幂与根式可以互化,通常利用分数指数幂进行根式的运算。 (2)有理数指数幂的性质 ①a r a s =a r+s (a 〉0,r 、s ∈Q ); ②(a r )s =a rs (a 〉0,r 、s ∈Q ); ③(ab)r =a r b s (a 〉0,b 〉0,r ∈Q );. 3.指数函数的图象与性质 y=a x a 〉1 0 图象 定义域R 值域(0,+∞) 性质(1)过定点(0,1) (2)当x>0时,y〉1; x〈0时,0 讲义 教材与考点分析: 本节课学习的内容是了解幂函数的图像及性质,如果a取非零的有理数是比较容易理解的,不过初学者对于a取无理数,则不太容易理解,在我们的课程里,不要求掌握如何理解指数为无理数的问题,因为这涉及到实数连续统的极为深刻的知识。因此我们只要接受它作为一个已知事实即可。 幂函数 一般地,形如y=x a x(a为实数)的函数叫幂函数对于a的取值为非零有理数,有必要分成几种情况来讨论各自的特性: 首先我们知道如果a=p/q,q和p都是整数,则x^(p/q)=q次根号(x的p 次方),如果q是奇数,函数的定义域是R,如果q是偶数,函数的定义域是[0,+∞)。当指数n是负整数时,设a=-k,则x=1/(x^k),显然x≠0,函数的定义域是(-∞,0)∪(0,+∞).因此可以看到x所受到的限制来源于两点,一是有可能作为分母而不能是0,一是有可能在偶数次的根号下而不能为负数,那么我们就可以知道: 排除了为0与负数两种可能,即对于x>0,则a可以是任意实数; 排除了为0这种可能,即对于x<0和x>0的所有实数,q不能是偶数; 排除了为负数这种可能,即对于x为大于且等于0的所有实数,a就不能是负数。 总结起来,就可以得到当a为不同的数值时,幂函数的定义域的不同情况如下:如果a为任意实数,则函数的定义域为大于0的所有实数; 如果a为负数,则x肯定不能为0,不过这时函数的定义域还必须根据q的奇偶性来确定,即如果同时q为偶数,则x不能小于0,这时函数的定义域为大于0的所有实数;如果同时q为奇数,则函数的定义域为不等于0 的所有实数。 在x大于0时,函数的值域总是大于0的实数。 在x小于0时,则只有同时q为奇数,函数的值域为非零的实数。 而只有a为正数,0才进入函数的值域。 由于x大于0是对a的任意取值都有意义的,因此下面给出幂函数在第一象限的各自情况. 可以看到: (1)所有的图形都通过(1,1)这点。 (2)当a大于0时,幂函数为单调递增的,而a小于0时,幂函数为单调递减函数。 (3)当a大于1时,幂函数图形下凹;当a小于1大于0时,幂函数图形上凸。(4)当a小于0时,a越小,图形倾斜程度越大。 (5)a大于0,函数过(0,0);a小于0,函数不过(0,0)点。 (6)显然幂函数无界。 练习:指数函数、对数函数、幂函数的图像与性质.doc
幂函数的图像与性质
3. 指对幂函数图像及其性质(文-中档)
最新幂函数的性质、常考题型及对应练习
幂函数的图像与性质
(完整版)幂函数的图像与性质(2)
幂函数的图像与性质
(完整版)幂函数图象及其性质
幂函数的性质与图像教案
指数函数、对数函数、幂函数的图像和性质知识点总结
幂函数的图象及性质
指数函数对数函数幂函数的图像与性质
幂函数的图像与性质
幂函数图象及其性质
指数函数对数函数幂函数的图像和性质知识点总结完整版
指数函数对数函数幂函数的图像和性质知识点总结
指数函数对数函数幂函数的图像和性质知识点总结
幂函数的图像及性质
相关文档
- 幂函数图象及其性质
- 最新幂函数的性质、常考题型及对应练习
- 指数函数、对数函数、幂函数的图像和性质知识点总结
- 幂函数的图像与性质优秀课件
- 幂函数图像和性质
- 幂函数图像和性质优秀课件
- 幂函数的图像与性质
- 幂函数图像与性质
- 指数函数对数函数幂函数的图像和性质知识点总结
- 指数函数、对数函数、幂函数的图像与性质.doc
- 幂函数图像与性质
- 5、幂函数图像与性质
- 指数函数,对数函数,幂函数的图像与性质
- 幂函数的图像与性质
- 指数函数对数函数幂函数的图像和性质知识点总结
- 幂函数性质图像 ppt课件
- 幂函数的图像及性质
- 幂函数的图像与性质
- 指数函数、对数函数、幂函数的图像和性质知识点总结
- 指数函数、对数函数、幂函数的图像与性质
